题目内容
设函数f(x)=lnx+
x2-(m+2)x,在x=a和x=b处有两个极值点,其中a<b,m∈R.
(Ⅰ)求实数m的取值范围;
(Ⅱ)若
≥e(e为自然对数的底数),求f(b)-f(a)的最大值.
| 1 |
| 2 |
(Ⅰ)求实数m的取值范围;
(Ⅱ)若
| b |
| a |
考点:利用导数求闭区间上函数的最值,利用导数研究函数的单调性
专题:导数的综合应用
分析:(Ⅰ)函数有两个极值点,结合定义域,知其导数有两个正实数根,得到不等式组,求出m的范围;
(Ⅱ)由题知a,b是两个极值点,结合韦达定理,得到f(b)-f(a)关于a,b的关系式,再用换元t=
,构造关于t的函数,求出g(t)的最大值.
(Ⅱ)由题知a,b是两个极值点,结合韦达定理,得到f(b)-f(a)关于a,b的关系式,再用换元t=
| b |
| a |
解答:
解:(Ⅰ) f′(x)=
,
则由题意得方程x2-(m+2)x+1=0有两个正根,
故
,
解得m>0.故实数m的取值范围是m>0.
(Ⅱ)f(b)-f(a)=ln
+
(b2-a2)-(m+2)(b-a),
又m+2=a+b,ab=1∴f(b)-f(a)=ln
-
(b2-a2)=ln
-
(
)=ln
-
(
-
),
设t=
(t≥e),故,构造函数g(t)=lnt-
(t-
)(t≥e)
g′(t)=
-
(1+
)=-
<0,
所以g(t)在[e,+∞)上是减函数,g(t)≤g(e)=1-
+
,
f(b)-f(a)的最大值为1-
+
.
| x2-(m+2)x+1 |
| x |
则由题意得方程x2-(m+2)x+1=0有两个正根,
故
|
解得m>0.故实数m的取值范围是m>0.
(Ⅱ)f(b)-f(a)=ln
| b |
| a |
| 1 |
| 2 |
又m+2=a+b,ab=1∴f(b)-f(a)=ln
| b |
| a |
| 1 |
| 2 |
| b |
| a |
| 1 |
| 2 |
| b2-a2 |
| ab |
| b |
| a |
| 1 |
| 2 |
| b |
| a |
| a |
| b |
设t=
| b |
| a |
| 1 |
| 2 |
| 1 |
| t |
g′(t)=
| 1 |
| t |
| 1 |
| 2 |
| 1 |
| t2 |
| (t-1)2 |
| 2t2 |
所以g(t)在[e,+∞)上是减函数,g(t)≤g(e)=1-
| e |
| 2 |
| 1 |
| 2e |
f(b)-f(a)的最大值为1-
| e |
| 2 |
| 1 |
| 2e |
点评:本题考查了,极值,韦达定理,换元法,以及构造思想.属于中档题.

练习册系列答案
相关题目
设离散型随机变量ξ的概率分布如下:则表中的a的值为( )
| ξ | 1 | 2 | 3 | 4 | ||||||
| P |
|
|
| a |
| A、1 | ||
B、
| ||
C、
| ||
D、
|
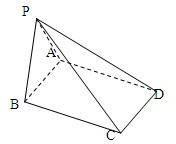 如图,四棱锥P-ABCD的底面是AB=2,BC=
如图,四棱锥P-ABCD的底面是AB=2,BC=