题目内容
已知集合m={x∈Z|-x2+6x＞0}，N={x|x2-5＜0}，则M∩N等于（ ）
| A、{1，2，3} |
| B、{1，2} |
| C、{2，3} |
| D、{3，4} |
考点：交集及其运算
专题：集合
分析：求出M中不等式的整数解确定出M，求出N中不等式的解集确定出N，找出M与N的交集即可．
解答：
解：由M中不等式变形得：x（x-6）＜0，
解得：0＜x＜6，即M={1，2，3，4，5}；
由N中不等式解得：-
＜x＜
，即N=（-
，
），
则M∩N={1，2}．
故选：B．
解得：0＜x＜6，即M={1，2，3，4，5}；
由N中不等式解得：-
| 5 |
| 5 |
| 5 |
| 5 |
则M∩N={1，2}．
故选：B．
点评：此题考查了交集及其运算，熟练掌握交集的定义是解本题的关键．
练习册系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
集合A={x|-1≤2x+1≤3}，B={x|x（x-2）≤0}，则A∩B=（ ）
| A、{x|-1≤x＜0} |
| B、{x|0＜x≤1} |
| C、{x|0≤x≤2} |
| D、{x|0≤x≤1} |
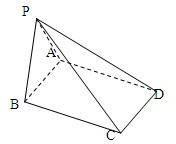如图，四棱锥P-ABCD的底面是AB=2，BC=