��Ŀ����
12�������������⣺�ٺ���$y=2{cos^2}��\frac{1}{3}x+\frac{��}{4}��-1$���溯����
�ڴ���ʵ������ʹ��$in��+cos��=\frac{3}{2}$��
�����������ǵ�һ�����Ҧ����£���tan����tan�£�
��$x=\frac{��}{8}$�Ǻ���$y=sin��2x+\frac{5��}{4}��$��һ���Գ��᷽�̣�
�ݺ���$y=sin��2x+\frac{��}{3}��$��ͼ����ڵ�$��\frac{��}{12}��0��$�����ĶԳ�ͼ�Σ�
����������ȷ���Ǣ٢ۢܣ�����ţ���
���� ���ɽ��ݹ�ʽ�����жϼ��ɣ�
�ڿ���sin��+cos��=$\sqrt{2}$sin��x+$\frac{��}{4}$����$\sqrt{2}$�жϣ�
�۸������к�����ͼ���жϼ��ɣ�
�ܢݸ��ݶԳ���ͶԳ����ĵ������жϣ�
��� �⣺�ٺ���$y=2{cos^2}��\frac{1}{3}x+\frac{��}{4}��-1$
=-sin$\frac{2x}{3}$�����溯������ȷ��
�ڴ���ʵ������ʹ��sin��+cos��=$\sqrt{2}$sin����+$\frac{��}{4}$����$\sqrt{2}$���ʴ���
�����������ǵ�һ�����Ҧ����£���tan����tan�£���Ȼ������
��$x=\frac{��}{8}$�Ǻ���$y=sin��2x+\frac{5��}{4}��$��f��$\frac{��}{8}$��=-1����һ���Գ��᷽�̣�����ȷ��
�ݺ���$y=sin��2x+\frac{��}{3}��$��ͼ����ڵ�$��\frac{��}{12}��0��$��f��$\frac{��}{12}$��=1�����ǶԳ����ģ��ʴ���
�ʴ�Ϊ�٢ۢܣ�
���� ���⿼�������Ǻ���ͼ������ʣ����ݹ�ʽ��ͬ�ǵ��������ҺͲ����⣬���ڻ������ͣ�Ӧ�������գ�

��ϰ��ϵ�д�
�����Ŀ
2��ij�����������ͼ��ͼ��ʾ����ü�����������ı����Ϊ��������
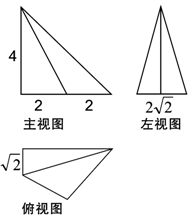

| A�� | 136�� | B�� | 144�� | C�� | 36�� | D�� | 34�� |
3��ִ����ͼ��ʾ�ij����ͼ������Ľ��Ϊ��������
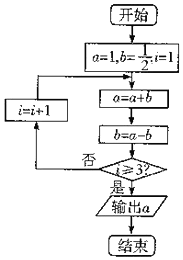

| A�� | 1 | B�� | 2 | C�� | 3 | D�� | 4 |
20���÷�֤��֤�����⡰��a2+b2=0��a��b��R������a��bȫΪ0�����䷴����ȷ���ǣ�������
| A�� | a��b������һ��Ϊ0 | B�� | a��b������һ����Ϊ0 | ||
| C�� | a��bȫ��Ϊ0 | D�� | a��b��ֻ��һ��Ϊ0 |
7����֪$\overrightarrow a��\overrightarrow b$��Ϊ��λ�������������ǵļн�Ϊ120�㣬��ô$|{\overrightarrow a-2\overrightarrow b}|$���ڣ�������
| A�� | $\sqrt{3}$ | B�� | $\sqrt{7}$ | C�� | 3 | D�� | 7 |
4��������ͼ��ʾ�ij����ͼ�����i��S��ֵ�ֱ�Ϊ��������


| A�� | 2��15 | B�� | 2��7 | C�� | 3��15 | D�� | 3��7 |
1����֪����x��y��һ��۲����������ʾ��
�ݴ˵õ��Ļع鷽��Ϊ$\stackrel{��}{y}$=$\stackrel{��}{b}$x+$\stackrel{��}{a}$����$\stackrel{��}{a}$=7.9����xÿ����1����λ��y��Ԥ��ֵ�ͣ�������
| x | 3 | 4 | 5 | 6 | 7 |
| y | 4.0 | 2.5 | -0.5 | 0.5 | -2.0 |
| A�� | ����1.4����λ | B�� | ����1.4����λ | C�� | ����1.2����λ | D�� | ����1.2����λ |