复数$z=\frac{{{{(i-1)}^2}+2}}{i+1}$的实部为0．题目和参考答案——青夏教育精英家教网—

题目内容

17．复数$z=\frac{{{{（i-1）}^2}+2}}{i+1}$的实部为0．

分析利用复数代数形式的乘除运算化简得答案．

解答解：∵$z=\frac{{{{（i-1）}^2}+2}}{i+1}$=$\frac{-2i+2}{1+i}=\frac{2（1-i）^{2}}{（1+i）（1-i）}=\frac{2×（-2i）}{2}=-2i$，
∴复数$z=\frac{{{{（i-1）}^2}+2}}{i+1}$的实部为0．
故答案为：0．

点评本题考查复数代数形式的乘除运算，考查了复数的基本概念，是基础题．

练习册系列答案

相关题目

7．

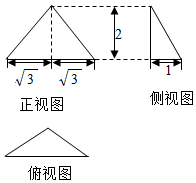已知一个三棱锥的三视图如下图所示，其中俯视图是顶角为$\frac{2π}{3}$的等腰三角形，则该三棱锥外接球的表面积为（　　）

8．已知命题p：a≤x≤a+1，命题q：x²-4x＜0，若p是q的充分不必要条件，则a的取值范围是（0，3）．

5．若复数z满足z=i（2-z）．
（1）求z；
（2）求|z-（2-i）|．

12．给出下列命题：
①函数$y=2{cos^2}（\frac{1}{3}x+\frac{π}{4}）-1$是奇函数；
②存在实数α，使得$inα+cosα=\frac{3}{2}$；
③若α，β是第一象限角且α＜β，则tanα＜tanβ；
④$x=\frac{π}{8}$是函数$y=sin（2x+\frac{5π}{4}）$的一条对称轴方程；
⑤函数$y=sin（2x+\frac{π}{3}）$的图象关于点$（\frac{π}{12}，0）$成中心对称图形．
其中命题正确的是①③④（填序号）．

2．在直角坐标系xoy中，以坐标原点为极点，x轴的非负半轴为极轴建立极坐标系，圆C的极坐标方程为ρ=4cosθ．
（1）求出圆C的直角坐标方程；
（2）已知圆C与x轴相交于A，B两点，若直线l：y=2x+2m上存在点P使得∠APB=90°，求实数m的最大值．

9．在复平面内，复数4+5i，-2+i对应的点分别为A，B，若C为线段AB的中点，则点C对应的复数是（　　）

6．设x∈R，向量$\overrightarrow a=（x，1）$，$\overrightarrow b=（1，-2）$，且$\overrightarrow a⊥\overrightarrow b$，则$\overrightarrow a$在$\overrightarrow a+\overrightarrow b$上的投影为$\frac{\sqrt{10}}{2}$．

7．“金导电、银导电、铜导电、锡导电，所以一切金属都导电”．此推理方法是（　　）

试题分类