题目内容
2.某品牌电动汽车的耗电量y与速度x之间满足的关系式为y=$\frac{1}{3}$x3-$\frac{39}{2}$x2-40x(x>0),为使耗电量最小,则速度为( )| A. | 30 | B. | 40 | C. | 50 | D. | 60 |
分析 欲求使耗电量最小,则其速度应定为多少,即求出函数的最小值即可,对函数求导,利用导数求研究函数的单调性,判断出最小值位置,代入算出结果.
解答 解:由题设知y'=x2-39x-40,
令y'>0,解得x>40,或x<-1,
故函数y=$\frac{1}{3}$x3-$\frac{39}{2}$x2-40x(x>0)在[40,+∞)上增,在(0,40]上减,
当x=40,y取得最小值.
由此得为使耗电量最小,则其速度应定为40;
故选:B.
点评 考查用导数研究函数的单调性求最值,本题是导数一章中最基本的应用题型.

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
10.将二进制数10110(2)化为十进制数结果为( )
| A. | 19 | B. | 22 | C. | 44 | D. | 14 |
17.设D=$\sqrt{{{({x-a})}^2}+{{({lnx-\frac{a^2}{4}})}^2}}+\frac{a^2}{4}$+1.(a∈R),则D的最小值为( )
| A. | $\frac{{\sqrt{2}}}{2}$ | B. | 1 | C. | $\sqrt{2}$ | D. | 2 |
7.“金导电、银导电、铜导电、锡导电,所以一切金属都导电”.此推理方法是( )
| A. | 完全归纳推理 | B. | 归纳推理 | C. | 类比推理 | D. | 演绎推理 |
14.上面图给出的是计算1+2+4+…+22017的值的一个程序框图,则其中判断框内应填入的是( ) 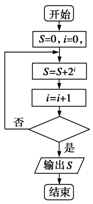

| A. | i=2017? | B. | i≥2017? | C. | i≥2018? | D. | i≤2018? |
12.若直线ax-by+2=0 (a>0,b>0)被圆x2+y2+2x-4y+1=0截得的弦长为4,则$\frac{1}{a}$+$\frac{1}{b}$的最小值为( )
| A. | $\frac{3}{2}$+$\sqrt{2}$ | B. | $\sqrt{2}$ | C. | $\frac{1}{4}$ | D. | $\frac{3}{2}$+2$\sqrt{2}$ |