题目内容
7.已知$\overrightarrow a,\overrightarrow b$均为单位向量,并且它们的夹角为120°,那么$|{\overrightarrow a-2\overrightarrow b}|$等于( )| A. | $\sqrt{3}$ | B. | $\sqrt{7}$ | C. | 3 | D. | 7 |
分析 运用向量数量积的定义可得$\overrightarrow{a}•\overrightarrow{b}$=|$\overrightarrow{a}$|•|$\overrightarrow{b}$|cos120°=1×1×(-$\frac{1}{2}$)=-$\frac{1}{2}$,再由向量的平方即为模的平方,化简整理计算即可得到所求值
解答 解:∵$\overrightarrow a,\overrightarrow b$均为单位向量,并且它们的夹角为120°,
∴|$\overrightarrow{a}$|=|$\overrightarrow{b}$|=1,$\overrightarrow{a}•\overrightarrow{b}$=|$\overrightarrow{a}$|•|$\overrightarrow{b}$|cos120°=1×1×(-$\frac{1}{2}$)=-$\frac{1}{2}$,
∴$|{\overrightarrow a-2\overrightarrow b}|$2=|$\overrightarrow{a}$|2+4|$\overrightarrow{b}$|2-4$\overrightarrow{a}•\overrightarrow{b}$=1+4+2=7,
∴$|{\overrightarrow a-2\overrightarrow b}|$=$\sqrt{7}$,
故选:B.
点评 本题考查向量的数量积的定义和性质,主要是向量的平方即为模的平方,考查运算能力,属于基础题.

练习册系列答案
 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
17.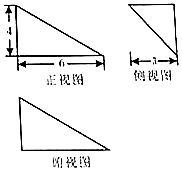 某几何体的三视图如图.若该几何体的顶点都在球O的表面上,则球O的体积是( )
某几何体的三视图如图.若该几何体的顶点都在球O的表面上,则球O的体积是( )
 某几何体的三视图如图.若该几何体的顶点都在球O的表面上,则球O的体积是( )
某几何体的三视图如图.若该几何体的顶点都在球O的表面上,则球O的体积是( )| A. | $\frac{\sqrt{61}}{6}$π | B. | $\frac{\sqrt{61}}{24}$π | C. | $\frac{61\sqrt{61}}{2}$π | D. | $\frac{61\sqrt{61}}{6}$π |
15.某地区最近十年粮食需求量逐年上升,下表是部分统计数据:
(1)利用所给数据求年需求量y与年份x之间的线性回归方程$\hat y=\hat bx+\hat a$.
(2)利用(1)中所求出的线性回归方程预测该地区2016年的粮食需求量.
(附:$\hat b=\frac{{\sum_{i=1}^n{({x_i}-\bar x)({y_i}-\bar y)}}}{{\sum_{i=1}^n{{{({x_i}\bar-\bar x)}^2}}}},\hat a=\bar y-\hat b\bar x$)
| 年份x | 2010 | 2011 | 2012 | 2013 | 2014 |
| 需求量y万吨 | 236 | 246 | 257 | 276 | 286 |
(2)利用(1)中所求出的线性回归方程预测该地区2016年的粮食需求量.
(附:$\hat b=\frac{{\sum_{i=1}^n{({x_i}-\bar x)({y_i}-\bar y)}}}{{\sum_{i=1}^n{{{({x_i}\bar-\bar x)}^2}}}},\hat a=\bar y-\hat b\bar x$)
17.设D=$\sqrt{{{({x-a})}^2}+{{({lnx-\frac{a^2}{4}})}^2}}+\frac{a^2}{4}$+1.(a∈R),则D的最小值为( )
| A. | $\frac{{\sqrt{2}}}{2}$ | B. | 1 | C. | $\sqrt{2}$ | D. | 2 |
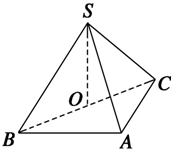 如图所示,在三棱锥S-ABC中,SO⊥平面ABC,侧面SAB与SAC均为等边三角形,∠BAC=90°,O为BC的中点,求二面角A-SC-B的余弦值.
如图所示,在三棱锥S-ABC中,SO⊥平面ABC,侧面SAB与SAC均为等边三角形,∠BAC=90°,O为BC的中点,求二面角A-SC-B的余弦值.