题目内容
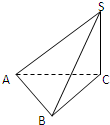
在空间四面体SABC中，SC⊥AB，AC⊥SC，且△ABC是锐角三角形，那么必有（ ）
| A、平面SAC⊥平面SCB |
| B、平面SAB⊥平面ABC |
| C、平面SCB⊥平面ABC |
| D、平面SAC⊥平面SAB |
考点：平面与平面垂直的判定
专题：空间位置关系与距离
分析：根据线线垂直得到线面垂直，再根据线在面内，得出面面垂直．
解答：
解：∵SC⊥AB，AC⊥SC，AC∩AB=A
∴SC⊥平面ABC，
又SC?平面SCB，SC?平面SAC
∴平面SCB⊥平面ABC，平面SAC⊥平面ABC
故选：C．
∴SC⊥平面ABC，
又SC?平面SCB，SC?平面SAC
∴平面SCB⊥平面ABC，平面SAC⊥平面ABC
故选：C．
点评：本题主要考查了面面垂直的判定定理，关键是找线面的关系，属于基础题．
练习册系列答案
相关题目
如图，AB是圆的直径，PA垂直于圆所在平面，C是圆周上不同于A，B的任意一点，在多面体P-AB的各个面中，共有直角三角形（ ）个．已知复数z1=cosα+isinα和复数z2=cosβ+isinβ，则复数z1•z2的实部是（ ）
| A、sin（α-β） |
| B、sin（α+β） |
| C、cos（α-β） |
| D、cos（α+β） |
对任意的x∈R，函数f（x）=x3+ax2+7ax不存在极值点的充要条件是（ ）
| A、a=0或a=7 |
| B、a＜0或a＞21 |
| C、0≤a≤21 |
| D、a=0或a=21 |
椭圆a2x2-
y2=1的一个焦点是（-2，0），则a等于（ ）
| a |
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
等比数列{an}的各项均为正数，且a4a5+a3a6=18，则log3a1+log3a2+…+log3a8=（ ）
| A、12 | B、10 | C、8 | D、6 |
下列命题是真命题的是（ ）
| A、a＞b是ac2＞bc2的充要条件 |
| B、a＞1，b＞1是ab＞1的充分条件 |
| C、?x0∈R，e x0≤0 |
| D、若p∨q为真命题，则p∧q为真 |
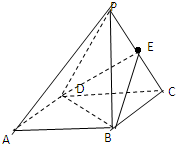如图，在四棱锥P-ABCD中，底面ABCD为正方形，E是PC的中点，