题目内容
下列命题是真命题的是（ ）
| A、a＞b是ac2＞bc2的充要条件 |
| B、a＞1，b＞1是ab＞1的充分条件 |
| C、?x0∈R，e x0≤0 |
| D、若p∨q为真命题，则p∧q为真 |
考点：复合命题的真假,特称命题
专题：简易逻辑
分析：利用复合命题的真假，充要条件以及特称命题判断结果即可．
解答：
解：对于A，a＞b推不出ac2＞bc2，说a＞b是ac2＞bc2的充要条件，不正确．
对于B，a＞1，b＞1⇒ab＞1的充分条件，正确．
对于C，由指数函数的值域可知：?x0∈R，e x0≤0是错误的．
对于D，若p∨q为真命题，则p∧q为真，有复合命题的真假判断，D不正确．
故选：B．
对于B，a＞1，b＞1⇒ab＞1的充分条件，正确．
对于C，由指数函数的值域可知：?x0∈R，e x0≤0是错误的．
对于D，若p∨q为真命题，则p∧q为真，有复合命题的真假判断，D不正确．
故选：B．
点评：本题考查命题的真假的判断与应用，充要条件以及特称命题的判断．
练习册系列答案
相关题目
记等差数列{an}的前n项和为Sn，利用倒序求和的方法得Sn=
；类似地，记等比数列{bn}的前n项积为Tn，且bn＞0（n∈N*），类比等差数列求和的方法，可将Tn表示成关于首项b1，末项bn与项数n的关系式为（ ）
| n(a1+an) |
| 2 |
A、
| |||||
B、
| |||||
C、
| |||||
D、
|
下列推理是归纳推理的是（ ）
| A、A，B为定点，动点P满足|PA|+|PB|=2a＞|AB|，则P点的轨迹为椭圆 | ||||
| B、由a1=1，an=3n-1，求出S1，S2，S3，猜想出数列的前n项和Sn的表达式 | ||||
C、由圆x2+y2=r2的面积πr2，猜想出椭圆
| ||||
| D、以上均不正确 |
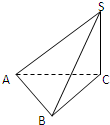
在空间四面体SABC中，SC⊥AB，AC⊥SC，且△ABC是锐角三角形，那么必有（ ）
| A、平面SAC⊥平面SCB |
| B、平面SAB⊥平面ABC |
| C、平面SCB⊥平面ABC |
| D、平面SAC⊥平面SAB |
一条直线与一个平面垂直的条件是（ ）
| A、垂直于平面内的一条直线 |
| B、垂直于平面内的两条直线 |
| C、垂直于平面内的无数条直线 |
| D、垂直于平面内的两条相交直线 |
已知直线l⊥平面α，直线m⊆平面β，给出下列命题，其中正确的是（ ）
①α∥β⇒l⊥m
②α⊥β⇒l∥m
③l∥m⇒α⊥β
④l⊥m⇒α∥β
①α∥β⇒l⊥m
②α⊥β⇒l∥m
③l∥m⇒α⊥β
④l⊥m⇒α∥β
| A、②④ | B、②③④ |
| C、①③ | D、①②③ |