题目内容
对任意的x∈R，函数f（x）=x3+ax2+7ax不存在极值点的充要条件是（ ）
| A、a=0或a=7 |
| B、a＜0或a＞21 |
| C、0≤a≤21 |
| D、a=0或a=21 |
考点：函数在某点取得极值的条件
专题：函数的性质及应用
分析：由于函数f（x）=x3+ax2+7ax（x∈R）不存在极值，可得f′（x）≥0恒成立，求解出一元二次不等式即可得到a的取值范围．
解答：
解：∵函数f（x）=x3+ax2+7ax（x∈R），
∴f′（x）=3x2+2ax+7a，
∵函数f（x）=x3+ax2+7ax（x∈R）不存在极值，且f′（x）的图象开口向上，
∴f′（x）≥0对x∈R恒成立，
∴△=4a2-84a≤0，
解得0≤a≤21，
∴a的取值范围是0≤a≤21．
故选：C．
∴f′（x）=3x2+2ax+7a，
∵函数f（x）=x3+ax2+7ax（x∈R）不存在极值，且f′（x）的图象开口向上，
∴f′（x）≥0对x∈R恒成立，
∴△=4a2-84a≤0，
解得0≤a≤21，
∴a的取值范围是0≤a≤21．
故选：C．
点评：本题考查了利用导数研究函数的极值，解题时要注意运用极值点必定是导函数对应方程的根，而导函数对应方程的根不一定是极值点．考查了转化化归的数学思想方法．属于中档题．
练习册系列答案
名校课堂系列答案
相关题目
f（x）=2x+cosx在（-∞，+∞）上（ ）
| A、是增函数 | B、是减函数 |
| C、有最大值 | D、有最小值 |
若x0是函数f（x）=（
）x-x
的零点，则x0属于区间（ ）
| 1 |
| 2 |
| 1 |
| 3 |
| A、（-1，0） |
| B、（0，1） |
| C、（1，2） |
| D、（2，3） |
设a＞0，b＞0，则以下不等式中不一定成立的是（ ）
| A、a2+b2+2≥2a+2b | ||||
| B、ln（ab+1）≥0 | ||||
C、
| ||||
| D、a3+b3≥2ab2 |
下列推理是归纳推理的是（ ）
| A、A，B为定点，动点P满足|PA|+|PB|=2a＞|AB|，则P点的轨迹为椭圆 | ||||
| B、由a1=1，an=3n-1，求出S1，S2，S3，猜想出数列的前n项和Sn的表达式 | ||||
C、由圆x2+y2=r2的面积πr2，猜想出椭圆
| ||||
| D、以上均不正确 |
若集合M={y|y=2x}，P={x|y=
}，M∩P=（ ）
| x-1 |
| A、[1，+∞） |
| B、[0，+∞） |
| C、（0，+∞） |
| D、（1，+∞） |
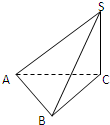
在空间四面体SABC中，SC⊥AB，AC⊥SC，且△ABC是锐角三角形，那么必有（ ）
| A、平面SAC⊥平面SCB |
| B、平面SAB⊥平面ABC |
| C、平面SCB⊥平面ABC |
| D、平面SAC⊥平面SAB |
已知直线l⊥平面α，直线m⊆平面β，给出下列命题，其中正确的是（ ）
①α∥β⇒l⊥m
②α⊥β⇒l∥m
③l∥m⇒α⊥β
④l⊥m⇒α∥β
①α∥β⇒l⊥m
②α⊥β⇒l∥m
③l∥m⇒α⊥β
④l⊥m⇒α∥β
| A、②④ | B、②③④ |
| C、①③ | D、①②③ |
如图，在四棱锥S-ABCD中，底面ABCD是直角梯形，AB⊥AD，AB⊥BC，侧棱SA⊥底面ABCD，点O为侧棱SC的中点，且SA=AB=BC=2，AD=1．