题目内容
如图，AB是圆的直径，PA垂直于圆所在平面，C是圆周上不同于A，B的任意一点，在多面体P-AB的各个面中，共有直角三角形（ ）个．| A、1 | B、2 | C、3 | D、4 |
考点：空间中直线与平面之间的位置关系
专题：空间位置关系与距离
分析：AB是圆O的直径，得出三角形ABC是直角三角形，由于PA垂直于圆O所在的平面，根据线面垂直的性质定理得出PA垂直于AC，BA，从而得出两个直角三角形，可以证明BC垂直于平面PAC，从而得出三角形PBC也是直角三角形，从而问题解决．
解答：
解：∵AB是圆O的直径，
∴∠ACB=90°即BC⊥AC，三角形ABC是直角三角形
又∵PA⊥圆O所在平面，
∴△PAC，△PAB是直角三角形．
且BC在这个平面内，
∴PA⊥BC 因此BC垂直于平面PAC中两条相交直线，
∴BC⊥平面PAC，
∴△PBC是直角三角形．
从而△PAB，△PAC，△ABC，△PBC中，直角三角形的个数是：4．
故选D．
∴∠ACB=90°即BC⊥AC，三角形ABC是直角三角形
又∵PA⊥圆O所在平面，
∴△PAC，△PAB是直角三角形．
且BC在这个平面内，
∴PA⊥BC 因此BC垂直于平面PAC中两条相交直线，
∴BC⊥平面PAC，
∴△PBC是直角三角形．
从而△PAB，△PAC，△ABC，△PBC中，直角三角形的个数是：4．
故选D．
点评：本题考查线面垂直的性质和判定定理的应用，要注意转化思想的应用，将线线垂直转化为线面垂直．
练习册系列答案
相关题目
设l，m表示两条不同的直线，α、β表示两个不同的平面，下列命题中真命题是（ ）
| A、若l?α，m∥α，则l∥m |
| B、若l?α，l∥m，则m∥α |
| C、若m∥α，m⊥β，则α⊥β |
| D、若m∥α，α⊥β，则m∥β |
f（x）=2x+cosx在（-∞，+∞）上（ ）
| A、是增函数 | B、是减函数 |
| C、有最大值 | D、有最小值 |
已知m，n为两条不同的直线，α，β为两个不同的平面，下列四个命题中，正确的是（ ）
| A、若m∥α，且n∥α，则m∥n |
| B、若m，n在α上，且m∥β，n∥β，则α∥β |
| C、若α⊥β，且m在α上，则m⊥β |
| D、若α⊥β，m⊥β，m在α外，则m∥α |
设集合M={x|
≤0}，N={x||x+1|≤2}，P={x|（
） x2+2x-3≥1}则有（ ）
| x+3 |
| x-1 |
| 1 |
| 2 |
| A、M⊆N=P |
| B、M⊆N⊆P |
| C、M=P⊆N |
| D、M=N=P |
记等差数列{an}的前n项和为Sn，利用倒序求和的方法得Sn=
；类似地，记等比数列{bn}的前n项积为Tn，且bn＞0（n∈N*），类比等差数列求和的方法，可将Tn表示成关于首项b1，末项bn与项数n的关系式为（ ）
| n(a1+an) |
| 2 |
A、
| |||||
B、
| |||||
C、
| |||||
D、
|
若x0是函数f（x）=（
）x-x
的零点，则x0属于区间（ ）
| 1 |
| 2 |
| 1 |
| 3 |
| A、（-1，0） |
| B、（0，1） |
| C、（1，2） |
| D、（2，3） |
在空间四面体SABC中，SC⊥AB，AC⊥SC，且△ABC是锐角三角形，那么必有（ ）
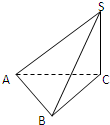
| A、平面SAC⊥平面SCB |
| B、平面SAB⊥平面ABC |
| C、平面SCB⊥平面ABC |
| D、平面SAC⊥平面SAB |