题目内容
椭圆a2x2-
y2=1的一个焦点是（-2，0），则a等于（ ）
| a |
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点：椭圆的简单性质
专题：计算题,圆锥曲线的定义、性质与方程
分析：先把椭圆方程化为标准方程，然后根据题意列一方程组，解出即可．
解答：
解：椭圆a2x2-
y2=1可化为
+
=1．
∵椭圆a2x2-
y2=1的一个焦点是（-2，0），
∴
-
=4，
∴a=
．
故选：B．
| a |
| 2 |
| x2 | ||
|
| y2 | ||
-
|
∵椭圆a2x2-
| a |
| 2 |
∴
| 1 |
| a2 |
| 2 |
| -a |
∴a=
1-
| ||
| 4 |
故选：B．
点评：本题考查椭圆的标准方程及简单性质，属基础题．
练习册系列答案
相关题目
已知m，n为两条不同的直线，α，β为两个不同的平面，下列四个命题中，正确的是（ ）
| A、若m∥α，且n∥α，则m∥n |
| B、若m，n在α上，且m∥β，n∥β，则α∥β |
| C、若α⊥β，且m在α上，则m⊥β |
| D、若α⊥β，m⊥β，m在α外，则m∥α |
若α是钝角，则θ=kπ+α，k∈Z是（ ）
| A、第二象限角 |
| B、第三象限角 |
| C、第二象限角或第三象限角 |
| D、第二象限角或第四象限角 |
下列推理是归纳推理的是（ ）
| A、A，B为定点，动点P满足|PA|+|PB|=2a＞|AB|，则P点的轨迹为椭圆 | ||||
| B、由a1=1，an=3n-1，求出S1，S2，S3，猜想出数列的前n项和Sn的表达式 | ||||
C、由圆x2+y2=r2的面积πr2，猜想出椭圆
| ||||
| D、以上均不正确 |
若函数y=x3-ax2+4在区间（0，2）内是单调递减函数，则实数a的取值范围是（ ）
| A、a≥3 | B、a=3 |
| C、a≤3 | D、0＜a＜3 |
在空间四面体SABC中，SC⊥AB，AC⊥SC，且△ABC是锐角三角形，那么必有（ ）
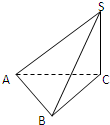
| A、平面SAC⊥平面SCB |
| B、平面SAB⊥平面ABC |
| C、平面SCB⊥平面ABC |
| D、平面SAC⊥平面SAB |
一条直线与一个平面垂直的条件是（ ）
| A、垂直于平面内的一条直线 |
| B、垂直于平面内的两条直线 |
| C、垂直于平面内的无数条直线 |
| D、垂直于平面内的两条相交直线 |
如图，在平行四边形ABCD中，|AB|=3，|BC|=2，