题目内容
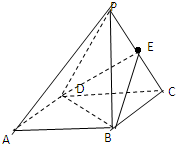如图，在四棱锥P-ABCD中，底面ABCD为正方形，E是PC的中点，求证：PA∥平面EDB．
考点：直线与平面平行的判定
专题：空间位置关系与距离
分析：由正方形的性质结合题意证出EO为△PBD的中位线，从而得到EO∥PA，利用线面平行的判定定理，即可证出PA∥平面EBD
解答：
证明：连接AC，与BD交于O，连接EO，因为底面ABCD为正方形，得O是AC的中点，
E是PC的中点，所以OE是三角形PAC的中位线，得EO∥PA，
又EO?平面EDB，PA?平面EDB
∴PA∥平面EDB
证明：连接AC，与BD交于O，连接EO，因为底面ABCD为正方形，得O是AC的中点，E是PC的中点，所以OE是三角形PAC的中位线，得EO∥PA，
又EO?平面EDB，PA?平面EDB
∴PA∥平面EDB
点评：本题在特殊的四棱锥中证明线面平行，着重考查了空间的平行的判定与证明的知识，属于中档题．
练习册系列答案
相关题目
若x0是函数f（x）=（
）x-x
的零点，则x0属于区间（ ）
| 1 |
| 2 |
| 1 |
| 3 |
| A、（-1，0） |
| B、（0，1） |
| C、（1，2） |
| D、（2，3） |
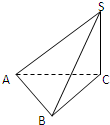
在空间四面体SABC中，SC⊥AB，AC⊥SC，且△ABC是锐角三角形，那么必有（ ）
| A、平面SAC⊥平面SCB |
| B、平面SAB⊥平面ABC |
| C、平面SCB⊥平面ABC |
| D、平面SAC⊥平面SAB |
已知直线l⊥平面α，直线m⊆平面β，给出下列命题，其中正确的是（ ）
①α∥β⇒l⊥m
②α⊥β⇒l∥m
③l∥m⇒α⊥β
④l⊥m⇒α∥β
①α∥β⇒l⊥m
②α⊥β⇒l∥m
③l∥m⇒α⊥β
④l⊥m⇒α∥β
| A、②④ | B、②③④ |
| C、①③ | D、①②③ |
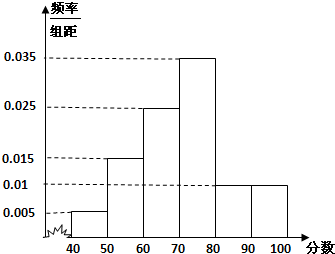
如图，在四棱锥S-ABCD中，底面ABCD是直角梯形，AB⊥AD，AB⊥BC，侧棱SA⊥底面ABCD，点O为侧棱SC的中点，且SA=AB=BC=2，AD=1．