题目内容
是否存在常数a、b,使等式:12+22+32+…+n2=an(n+b)(2n+1)对一切正整数n成立?并证明你的结论.
考点:数学归纳法
专题:证明题,点列、递归数列与数学归纳法
分析:先令n=1,n=2,构造三个方程求出a,b,再用用数学归纳法证明成立,证明时先证:(1)当n=1时成立.(2)再假设n=k(k≥1)时,成立,递推到n=k+1时,成立即可.
解答:
解:分别将n=1,2代人,得
,
∴a=
,b=1…(2分)
下面用数学归纳法证明
(1)当n=1时,由上可知等式成立…(3分)
(2)假设n=k时结论成立,即12+22+32+…+k2=
,
那么n=k+1时,12+22+32+…+k2+(k+1)2=
+(k+1)2
=
=
,
这就是说,n=k+1时,结论也成立…(11分)
由(1)(2)可知,存在常数a=
,b=1使等式:12+22+32+…+n2=an(n+b)(2n+1)对一切正整数n成立…(12分)
|
∴a=
| 1 |
| 6 |
下面用数学归纳法证明
(1)当n=1时,由上可知等式成立…(3分)
(2)假设n=k时结论成立,即12+22+32+…+k2=
| k(k+1)(2k+1) |
| 6 |
那么n=k+1时,12+22+32+…+k2+(k+1)2=
| k(k+1)(2k+1) |
| 6 |
=
| (k+1)(k+2)(2k+3) |
| 6 |
| (k+1)[(k+1)+1][2(k+1)+1] |
| 6 |
这就是说,n=k+1时,结论也成立…(11分)
由(1)(2)可知,存在常数a=
| 1 |
| 6 |
点评:本题主要考查研究存在性问题和数学归纳法,对存在性问题先假设存在,再证明是否符合条件,数学归纳法的关键是递推环节,要符合假设的模型才能成立.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
在空间四面体SABC中,SC⊥AB,AC⊥SC,且△ABC是锐角三角形,那么必有( )
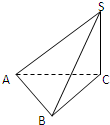

| A、平面SAC⊥平面SCB |
| B、平面SAB⊥平面ABC |
| C、平面SCB⊥平面ABC |
| D、平面SAC⊥平面SAB |
 如图,在四棱锥S-ABCD中,底面ABCD是直角梯形,AB⊥AD,AB⊥BC,侧棱SA⊥底面ABCD,点O为侧棱SC的中点,且SA=AB=BC=2,AD=1.
如图,在四棱锥S-ABCD中,底面ABCD是直角梯形,AB⊥AD,AB⊥BC,侧棱SA⊥底面ABCD,点O为侧棱SC的中点,且SA=AB=BC=2,AD=1. 如图,在平行四边形ABCD中,|AB|=3,|BC|=2,
如图,在平行四边形ABCD中,|AB|=3,|BC|=2,