题目内容
17.已知动直线l的方程:cosα•(x-2)+sinα•(y+1)=1(α∈R),给出如下结论:①动直线l恒过某一定点;
②存在不同的实数α1,α2,使相应的直线l1,l2平行;
③坐标平面上至少存在两个点都不在动直线l上;
④动直线l可表示坐标平面上除x=2,y=-1之外的所有直线;
⑤动直线l可表示坐标平面上的所有直线;
其中正确结论的序号是②③.
分析 ①,圆(x-2)2+(y+1)2=1上任一点P(2+cosα,-1+sinα),则点P处的切线为cosα•(x-2)+sinα•(y+1)=1(α∈R);
②,当≠0时,直线的斜率k=-$\frac{cosα}{sinα}=-cotα$,存在不同的实数α1,α1,使cotα1=cotα1,相应的直线l1,l2平行;
③,cosα•(x-2)+sinα•(y+1)=1⇒$\sqrt{(x-2)^{2}+(y-1)^{2}}sin(α+θ)=1$,所有使$\sqrt{(x-2)^{2}+(y-1)^{2}}<1$的点(x,y)都不在其上;
对于④,⑤由③可判定.
解答 解:对于①,圆(x-2)2+(y+1)2=1上任一点P(2+cosα,-1+sinα),则点P处的切线为cosα•(x-2)+sinα•(y+1)=1(α∈R),直线不会过一定点,故错;
对于②,当≠0时,直线的斜率k=-$\frac{cosα}{sinα}=-cotα$,存在不同的实数α1,α1,使cotα1=cotα1,相应的直线l1,l2平行,故正确;
对于③,cosα•(x-2)+sinα•(y+1)=1⇒$\sqrt{(x-2)^{2}+(y-1)^{2}}sin(α+θ)=1$,所有使$\sqrt{(x-2)^{2}+(y-1)^{2}}<1$的点(x,y)都不在其上,故正确;
对于④,⑤由③可得错.
故答案为:②③
点评 本题考查了命题真假的判定,涉及到直线方程的知识,属于基础题.

练习册系列答案
相关题目
8.某学校为了解学生的学习、生活等情况,决定召开一次学生座谈会.此学校各年级人数情况如表:
(1)若按年级用分层抽样的方法抽取n个人,其中高二年级22人,高三年级20人,再从这n个人中随机抽取出1人,此人为高三年级的概率为$\frac{10}{33}$,求x、y的值.
(2)若按性别用分层抽样的方法在高三年级抽取一个容量为5的样本,从这5人中任取2人,求至少有1人是男生的概率.
| 年 级 性 别 | 高一年级 | 高二年级 | 高三年级 |
| 男 | 520 | y | 400 |
| 女 | x | 610 | 600 |
(2)若按性别用分层抽样的方法在高三年级抽取一个容量为5的样本,从这5人中任取2人,求至少有1人是男生的概率.
5.过A(0,1),B(3,5)两点的直线的斜率是( )
| A. | $\frac{4}{3}$ | B. | $\frac{3}{4}$ | C. | $-\frac{4}{3}$ | D. | $-\frac{3}{4}$ |
12.能推出{an}是递增数列的是( )
| A. | {an}是等差数列且$\left\{{\frac{a_n}{n}}\right\}$递增 | |
| B. | Sn是等差数列{an}的前n项和,且$\left\{{\frac{S_n}{n}}\right\}$递增 | |
| C. | {an}是等比数列,公比为q>1 | |
| D. | 等比数列{an},公比为0<q<1 |
2.已知函数y=f(2x)+2x是偶函数,且f(2)=1,则f(-2)=( )
| A. | 5 | B. | 4 | C. | 3 | D. | 2 |
6.一梯形的直观图是如图是欧式的等腰梯形,且直观图OA′B′C′的面积为2,则原梯形的面积为( )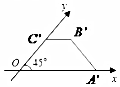

| A. | 2 | B. | 2$\sqrt{2}$ | C. | 4 | D. | 4$\sqrt{2}$ |
9.若tanα<0,则( )
| A. | sinα<0 | B. | cosα<0 | C. | sinαcosα<0 | D. | sinα-cosα<0 |
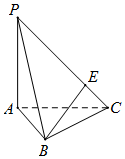 如图,在三棱锥P-ABC中,PA⊥平面ABC,AB=BC,PA=AC,E为PC上的动点,当 BE⊥PC时,$\frac{CE}{PC}$的值为$\frac{1}{4}$.
如图,在三棱锥P-ABC中,PA⊥平面ABC,AB=BC,PA=AC,E为PC上的动点,当 BE⊥PC时,$\frac{CE}{PC}$的值为$\frac{1}{4}$.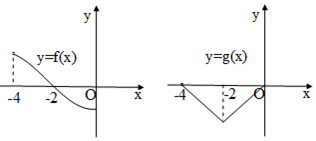 已知偶函数f(x)和奇函数g(x)的定义域都是(-4,4),且在(-4,0]上的图象如图所示,则关于x的不等式f(x)•g(x)<0的解集是(-4,-2)∪(0,2).
已知偶函数f(x)和奇函数g(x)的定义域都是(-4,4),且在(-4,0]上的图象如图所示,则关于x的不等式f(x)•g(x)<0的解集是(-4,-2)∪(0,2).