Question

6．一梯形的直观图是如图是欧式的等腰梯形，且直观图OA′B′C′的面积为2，则原梯形的面积为（　　）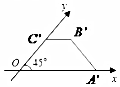

• A． 2
• B． 2$\sqrt{2}$
• C． 4
• D． 4$\sqrt{2}$

Answer 1

分析 把该梯形的直观图还原为原来的梯形，画出图形，结合图形解答问题即可．

解答 解：把该梯形的直观图还原为原来的梯形，如图所示；
设该梯形的上底为a，下底为b，高为h，
则直观图中等腰梯形的高为h′=$\frac{1}{2}$hsin45°；
∵等腰梯形的体积为$\frac{1}{2}$（a+b）h′=$\frac{1}{2}$（a+b）•$\frac{1}{2}$hsin45°=2，
∴$\frac{1}{2}$（a+b）•h=$\frac{2}{\frac{1}{2}sin45°}$=4$\sqrt{2}$
∴该梯形的面积为4$\sqrt{2}$．
故选：D．

点评 本题考查了平面图形的直观图的画法与应用问题，解题时应明确直观图与原来图形的区别和联系，是基础题目．