题目内容
12.能推出{an}是递增数列的是( )| A. | {an}是等差数列且$\left\{{\frac{a_n}{n}}\right\}$递增 | |
| B. | Sn是等差数列{an}的前n项和,且$\left\{{\frac{S_n}{n}}\right\}$递增 | |
| C. | {an}是等比数列,公比为q>1 | |
| D. | 等比数列{an},公比为0<q<1 |
分析 利用等差数列与等比数列的通项公式求和公式及其单调性即可判断出结论.
解答 解:对于B:Sn=$n{a}_{1}+\frac{n(n-1)}{2}d$,$\frac{{S}_{n}}{n}$=a1+$\frac{n-1}{2}d$,
∵$\left\{{\frac{S_n}{n}}\right\}$递增,∴d>0,因此{an}是递增数列.
故选:B.
点评 本题考查了等差数列与等比数列的通项公式求和公式及其单调性,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
2.用一个平面去截一个几何体,得到的截面不可能是圆的几何体是( )
| A. | 圆锥 | B. | 圆柱 | C. | 球 | D. | 三棱锥 |
7.直线$\frac{x}{a}-\frac{y}{b}=1$在y轴上的截距是( )
| A. | a | B. | b | C. | -a | D. | -b |
4.记a=sin1,b=sin2,c=sin3,则( )
| A. | c<b<a | B. | c<a<b | C. | a<c<b | D. | a<b<c |
4. “健步走”是一种方便而又有效的锻炼方式,李老师每天坚持“健步走”,并用计步器进行统计.他最近8天“健步走”步数的条形统计图及相应的消耗能量数据表如表:
“健步走”是一种方便而又有效的锻炼方式,李老师每天坚持“健步走”,并用计步器进行统计.他最近8天“健步走”步数的条形统计图及相应的消耗能量数据表如表:
(1)求李老师这8天“健步走”步数的平均数;
(2)从步数为16千步,17千步,18千步的6天中任选2天,设李老师这2天通过“健步走”消耗的能量和为X,求X的分布列及数学期望.
 “健步走”是一种方便而又有效的锻炼方式,李老师每天坚持“健步走”,并用计步器进行统计.他最近8天“健步走”步数的条形统计图及相应的消耗能量数据表如表:
“健步走”是一种方便而又有效的锻炼方式,李老师每天坚持“健步走”,并用计步器进行统计.他最近8天“健步走”步数的条形统计图及相应的消耗能量数据表如表:| 步数(千卡) | 16 | 17 | 18 | 19 |
| 消耗能量(卡路里) | 400 | 440 | 480 | 520 |
(2)从步数为16千步,17千步,18千步的6天中任选2天,设李老师这2天通过“健步走”消耗的能量和为X,求X的分布列及数学期望.
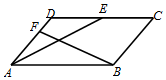 如图所示,在平行四边形ABCD中,AB=4,AD=3,E是边CD的中点,$\overrightarrow{DF}$=$\frac{1}{3}$$\overrightarrow{DA}$,若$\overrightarrow{AE}$•$\overrightarrow{BF}$=-4,则sin∠BAD=$\frac{\sqrt{15}}{4}$.
如图所示,在平行四边形ABCD中,AB=4,AD=3,E是边CD的中点,$\overrightarrow{DF}$=$\frac{1}{3}$$\overrightarrow{DA}$,若$\overrightarrow{AE}$•$\overrightarrow{BF}$=-4,则sin∠BAD=$\frac{\sqrt{15}}{4}$.