题目内容
7.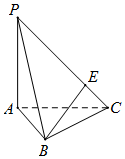 如图,在三棱锥P-ABC中,PA⊥平面ABC,AB=BC,PA=AC,E为PC上的动点,当 BE⊥PC时,$\frac{CE}{PC}$的值为$\frac{1}{4}$.
如图,在三棱锥P-ABC中,PA⊥平面ABC,AB=BC,PA=AC,E为PC上的动点,当 BE⊥PC时,$\frac{CE}{PC}$的值为$\frac{1}{4}$.
分析 取特殊值,设AB⊥BC,AB=BC=$\sqrt{2}$,以B为原点,BA为x轴,BC为y轴,过B作平面ABC的垂线为z轴,建立空间直角坐标系,利用向量法能求出当BE⊥PC时,$\frac{CE}{PC}$的值为$\frac{1}{4}$.
解答 解:取特殊值,设AB⊥BC,AB=BC=$\sqrt{2}$,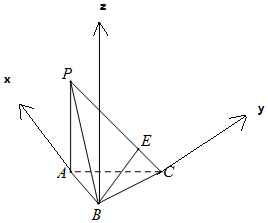
以B为原点,BA为x轴,BC为y轴,过B作平面ABC的垂线为z轴,建立空间直角坐标系,
则B(0,0,0),P($\sqrt{2}$,2,0),C(0,$\sqrt{2}$,0),
设E(a,b,c),$\frac{CE}{PC}$=λ(0≤λ≤1),
则$\overrightarrow{CE}=λ\overrightarrow{CP}$,即(a,b-$\sqrt{2}$,c)=λ($\sqrt{2},2-\sqrt{2}$,0),
∴$\left\{\begin{array}{l}{a=\sqrt{2}λ}\\{b=\sqrt{2}+(2-\sqrt{2})λ}\\{c=0}\end{array}\right.$,
∴E($\sqrt{2}λ,\sqrt{2}+(2-\sqrt{2})λ,0$),
∴$\overrightarrow{BE}$=($\sqrt{2}λ,\sqrt{2}+(2-\sqrt{2})λ,0$),$\overrightarrow{PC}$=(-$\sqrt{2}$,$\sqrt{2}-2$,0),
∵BE⊥PC,∴$\overrightarrow{BE}•\overrightarrow{PC}$=-2λ+$\sqrt{2}(\sqrt{2}-2)$-(2-$\sqrt{2}$)2λ=0,
解得$λ=\frac{1}{4}$.
∴当BE⊥PC时,$\frac{CE}{PC}$的值为$\frac{1}{4}$.
故答案为:$\frac{1}{4}$.
点评 本题考查线段的比值的求法,是中档题,解题时要认真审题,注意向量法的合理运用.

| A. | 圆锥 | B. | 圆柱 | C. | 球 | D. | 三棱锥 |
| A. | {-2,-1,0,1} | B. | {-2,-1,0} | C. | {-2,-1} | D. | {-1} |

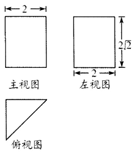 《九章算术》中将底面是直角三角形的直三棱柱称之为“堑堵”,已知某“堑堵”的三视图如图所示,则该“堑堵”的外接球的表面积为16π.
《九章算术》中将底面是直角三角形的直三棱柱称之为“堑堵”,已知某“堑堵”的三视图如图所示,则该“堑堵”的外接球的表面积为16π.