题目内容
8.某学校为了解学生的学习、生活等情况,决定召开一次学生座谈会.此学校各年级人数情况如表:| 年 级 性 别 | 高一年级 | 高二年级 | 高三年级 |
| 男 | 520 | y | 400 |
| 女 | x | 610 | 600 |
(2)若按性别用分层抽样的方法在高三年级抽取一个容量为5的样本,从这5人中任取2人,求至少有1人是男生的概率.
分析 (1)依题意得:$\frac{20}{n}=\frac{10}{33}$,求出n=66,从而得到高一年级被抽取的人数为24.由此能求出x,y.
(2)若用分层抽样的方法在高三年级抽取一个容量为5的样本,设抽取男生的人数为m,则$\frac{m}{5}=\frac{400}{600+400}$,解得m=2,从而应抽取男生2人,女生3人,分别记作A1、A2;B1、B2、B3,利用列举法能求出至少有1人是男生的概率.
解答 解:(1)依题意得:$\frac{20}{n}=\frac{10}{33}$,解得n=66.…(2分)
所以高一年级被抽取的人数为66-22-20=24.
所以$\frac{20}{1000}=\frac{24}{520+x}=\frac{22}{y+610}$,解得x=680,y=490.…(6分)
(2)若用分层抽样的方法在高三年级抽取一个容量为5的样本,
设抽取男生的人数为m,则$\frac{m}{5}=\frac{400}{600+400}$,解得m=2,
所以应抽取男生2人,女生3人,分别记作A1、A2;B1、B2、B3.…(8分)
记“从中任取2人,至少有1人是男生”为事件A.
从中任取2人的所有基本事件共10个:(A1,A2),(A1,B1),(A1,B2),(A1,B3),
(A2,B1),(A2,B2),(A2,B3),(B1,B2),(B1,B3),(B2,B3).
其中至少有1人为男生的基本事件有7个:
(A1,A2),(A1,B1),(A1,B2),(A1,B3),(A2,B1),(A2,B2),(A2,B3).
所以从中从中任取2人,至少有1人是男生的概率为$\frac{7}{10}$.…(13分)
∴至少有1人是男生的概率$\frac{7}{10}$.…(14分)
点评 本题考查实数值的求法,考查概率的求法,是基础题,解题时要认真审题,注意列举法的合理运用.

 名校课堂系列答案
名校课堂系列答案| A. | {-2,-1,0,1} | B. | {-2,-1,0} | C. | {-2,-1} | D. | {-1} |

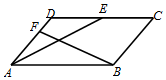 如图所示,在平行四边形ABCD中,AB=4,AD=3,E是边CD的中点,$\overrightarrow{DF}$=$\frac{1}{3}$$\overrightarrow{DA}$,若$\overrightarrow{AE}$•$\overrightarrow{BF}$=-4,则sin∠BAD=$\frac{\sqrt{15}}{4}$.
如图所示,在平行四边形ABCD中,AB=4,AD=3,E是边CD的中点,$\overrightarrow{DF}$=$\frac{1}{3}$$\overrightarrow{DA}$,若$\overrightarrow{AE}$•$\overrightarrow{BF}$=-4,则sin∠BAD=$\frac{\sqrt{15}}{4}$.