题目内容
9.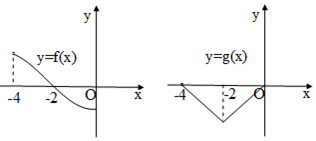 已知偶函数f(x)和奇函数g(x)的定义域都是(-4,4),且在(-4,0]上的图象如图所示,则关于x的不等式f(x)•g(x)<0的解集是(-4,-2)∪(0,2).
已知偶函数f(x)和奇函数g(x)的定义域都是(-4,4),且在(-4,0]上的图象如图所示,则关于x的不等式f(x)•g(x)<0的解集是(-4,-2)∪(0,2).
分析 令h(x)=f(x)g(x),根据h(x)的奇偶性和函数图象得出不等式的解.
解答 解:设h(x)=f(x)g(x),则h(-x)=f(-x)g(-x)=-f(x)g(x)=-h(x),
∴h(x)是奇函数,
由图象可知:当-4<x<-2时,f(x)>0,g(x)<0,即h(x)>0,
当0<x<2时,f(x)<0,g(x)>0,即h(x)<0,
∴h(x)<0的解为(-4,-2)∪(0,2).
故答案为(-4,-2)∪(0,2)
点评 本题考查了函数奇偶性的性质,函数图象的意义,属于中档题.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
19.已知集合A={x∈Z|(x+2)(x-1)<0},B={-2,-1},那么A∪B等于( )
| A. | {-2,-1,0,1} | B. | {-2,-1,0} | C. | {-2,-1} | D. | {-1} |
4.记a=sin1,b=sin2,c=sin3,则( )
| A. | c<b<a | B. | c<a<b | C. | a<c<b | D. | a<b<c |
14.如果函数y=sin(x+ϕ)的图象经过点$(\frac{π}{3},0)$,那么ϕ可以是( )
| A. | 0 | B. | $\frac{π}{6}$ | C. | $\frac{π}{3}$ | D. | $\frac{2π}{3}$ |
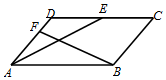 如图所示,在平行四边形ABCD中,AB=4,AD=3,E是边CD的中点,$\overrightarrow{DF}$=$\frac{1}{3}$$\overrightarrow{DA}$,若$\overrightarrow{AE}$•$\overrightarrow{BF}$=-4,则sin∠BAD=$\frac{\sqrt{15}}{4}$.
如图所示,在平行四边形ABCD中,AB=4,AD=3,E是边CD的中点,$\overrightarrow{DF}$=$\frac{1}{3}$$\overrightarrow{DA}$,若$\overrightarrow{AE}$•$\overrightarrow{BF}$=-4,则sin∠BAD=$\frac{\sqrt{15}}{4}$.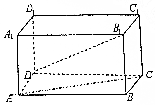 如图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2.
如图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2.