题目内容
9．若tanα＜0，则（ ）| A． | sinα＜0 | B． | cosα＜0 | C． | sinαcosα＜0 | D． | sinα-cosα＜0 |
分析 由tanα＜0，即$\frac{sinα}{cosα}＜0$，得到sina，cosa异号，从而逐个判断得答案．
解答 解：由tanα＜0，即$\frac{sinα}{cosα}＜0$，
∴sina，cosa异号，
∴sinα＜0，cosα＜0，sinα-cosα＜0都不正确；
∴sinαcosα＜0正确．
故选：C．
点评 本题考查了三角函数值的符号，是基础题．
练习册系列答案
相关题目
15．设函数f（x）=ax2+bx+c（a＞b＞c）的图象经过点A（m1，f（m1））和点B（m2，f（m2）），f（1）=0，若a2+（f（m1）+f（m2）•a+f（m1）•f（m2）=0，则（ ）
| A． | b≥0 | B． | b＜0 | C． | 3a+c≤0 | D． | 3a-c＜0 |
4．
“健步走”是一种方便而又有效的锻炼方式，李老师每天坚持“健步走”，并用计步器进行统计．他最近8天“健步走”步数的条形统计图及相应的消耗能量数据表如表：
（1）求李老师这8天“健步走”步数的平均数；
（2）从步数为16千步，17千步，18千步的6天中任选2天，设李老师这2天通过“健步走”消耗的能量和为X，求X的分布列及数学期望．
“健步走”是一种方便而又有效的锻炼方式，李老师每天坚持“健步走”，并用计步器进行统计．他最近8天“健步走”步数的条形统计图及相应的消耗能量数据表如表：| 步数（千卡） | 16 | 17 | 18 | 19 |
| 消耗能量（卡路里） | 400 | 440 | 480 | 520 |
（2）从步数为16千步，17千步，18千步的6天中任选2天，设李老师这2天通过“健步走”消耗的能量和为X，求X的分布列及数学期望．
14．已知$|{\overrightarrow{OA}}|=|{\overrightarrow{OB}}|=1$，且$\overrightarrow{OA}•\overrightarrow{OB}=0$，点C在∠AOB内，$\overrightarrow{OA}$与$\overrightarrow{OC}$夹角为30°，若$\overrightarrow{OC}=m\overrightarrow{OA}+n\overrightarrow{OB}$，（m，n∈R），则$\frac{n}{m}$的值为（ ）
| A． | $\frac{{\sqrt{3}}}{3}$ | B． | $\sqrt{2}$ | C． | $\sqrt{3}$ | D． | $\frac{{\sqrt{2}}}{2}$ |
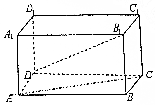如图，在长方体ABCD-A1B1C1D1中，AD=AA1=1，AB=2．