题目内容
函数f（x）=x-lnx的单调递减区间为（ ）
| A、（-∞，1） |
| B、（1，+∞） |
| C、（0，1） |
| D、（0，+∞） |
考点：利用导数研究函数的单调性
专题：导数的概念及应用
分析：先求出函数的导数，令导函数小于0，解不等式，进而求出函数的递减区间．
解答：
解：∵f′（x）=1-
=
，（x＞0），
令f′（x）＜0，解得：0＜x＜1，
∴f（x）在（0，1）递减，
故选：C．
| 1 |
| x |
| x-1 |
| x |
令f′（x）＜0，解得：0＜x＜1，
∴f（x）在（0，1）递减，
故选：C．
点评：本题考查了函数的单调性，考查导数的应用，是一道基础题．
练习册系列答案
相关题目
设
•
不共线，则下列四组向量中不能作为基底的是（ ）
| e1 |
| e2 |
A、
| ||||||||
B、3
| ||||||||
C、
| ||||||||
D、
|
设an=（n+1）2，bn=n2-n（n∈N*），则下列命题中不正确的是（ ）
| A、{an+1-an}是等差数列 |
| B、{bn+1-bn}是等差数列 |
| C、{an-bn}是等差数列 |
| D、{an+bn}是等差数列 |
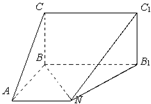如图五面体中，四边形CBB1C1为矩形，B1C1⊥平面ABB1N，四边形ABB1N为梯形，