题目内容
在△ABC中,AB=2,BC=1,∠ABC=60°.若使之绕直线BC旋转一周,则所形成的几何体的体积是( )
A、
| ||
| B、π | ||
| C、3π | ||
| D、9π |
考点:棱柱、棱锥、棱台的体积
专题:计算题,空间位置关系与距离
分析:由题意,△ABC为直角三角形,BC为直角边,故使之绕直线BC旋转一周得到的是圆锥,从而求体积.
解答:
解:由题意,
△ABC为直角三角形,
BC为直角边,
故使之绕直线BC旋转一周得到的是圆锥,
其底面圆的半径为
,
高为1,
故所形成的几何体的体积是
V=
×π×3×1=π,
故选B.
△ABC为直角三角形,
BC为直角边,
故使之绕直线BC旋转一周得到的是圆锥,
其底面圆的半径为
| 3 |
高为1,
故所形成的几何体的体积是
V=
| 1 |
| 3 |
故选B.
点评:本题考查了圆锥的形成与体积求法及学生的空间想象力,属于中档题.

练习册系列答案
相关题目
| 2sin23°cos23°-sin16°cos30° |
| cos′16° |
A、-
| ||||
B、-
| ||||
C、
| ||||
D、
|
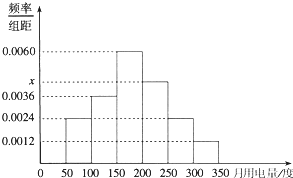 从某小区抽取100户居民进行月用电量调查,发现其用电量都在50到350度之间,频率分布直方图如图所示.求
从某小区抽取100户居民进行月用电量调查,发现其用电量都在50到350度之间,频率分布直方图如图所示.求
 已知△ABC中,A(2,-1),B(4,3),C(3,-2),求:
已知△ABC中,A(2,-1),B(4,3),C(3,-2),求: