题目内容
△ABC中,已知C(2,5),∠A的平分线所在的直线方程是y=x,BC边上高线所在的直线方程是y=2x-1,试求顶点B的坐标.
考点:直线的一般式方程与直线的垂直关系,两直线的夹角与到角问题
专题:直线与圆
分析:首先求出A点的坐标,进而求出AB边所在的直线方程,然后根据两直线垂直求出BC边所在的直线的斜率和方程,最后联立方程即可求出B得的坐标.
解答:
解:依条件,由
解得A(1,1).
因为∠A的平分线所在的直线方程是y=x,
所以点C(2,5)关于y=x的对称点C'(5,2)在边AB
所在的直线上.
所以AB边所在的直线方程为y-1=
(x-1)
整理得x-4y+3=0 …(6分)
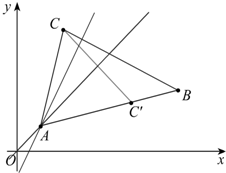
又BC边上高线所在的直线方程是y=2x-1
所以BC边所在的直线的斜率为-
.
BC边所在的直线的方程是y=-
(x-2)+5
整理得x+2y-12=0…(10分)
联立
,解得B(7,
)…(12分)
|
因为∠A的平分线所在的直线方程是y=x,
所以点C(2,5)关于y=x的对称点C'(5,2)在边AB
所在的直线上.
所以AB边所在的直线方程为y-1=
| 2-1 |
| 5-1 |
整理得x-4y+3=0 …(6分)

又BC边上高线所在的直线方程是y=2x-1
所以BC边所在的直线的斜率为-
| 1 |
| 2 |
BC边所在的直线的方程是y=-
| 1 |
| 2 |
整理得x+2y-12=0…(10分)
联立
|
| 5 |
| 2 |
点评:着重考查了直线的基本量与基本形式、直线的位置关系等知识,属于基础题.

练习册系列答案
 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案
相关题目
在△ABC中,AB=2,BC=1,∠ABC=60°.若使之绕直线BC旋转一周,则所形成的几何体的体积是( )
A、
| ||
| B、π | ||
| C、3π | ||
| D、9π |