Question

为了了解某地区高三学生的身体发育情况，抽查了该地区100名年龄为17.5岁～8岁的男生体重（kg），得到频率分布直方图如图：求：

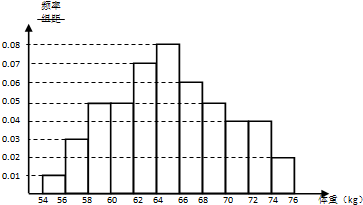
（1）根据直方图可得这100名学生中体重在（56，64）的学生人数；
（2）请根据上面的频率分布直方图估计该地区17.5-18岁的男生体重；
（3）若在这100名男生中随意抽取1人，该生体重低于62的概率是多少？

Answer 1

考点：频率分布直方图

专题：概率与统计

分析：（1）根据直方图求出这100名学生中体重在（56，64）的学生数；
（2）求出样本的平均数，利用平均数来衡量该地区17.5-18岁的男生体重；
（3）求出样本数据中低于62kg的频率，即是概率．

解答： 解：（1）根据直方图得，这100名学生中体重在（56，64）的学生人数为：
（0.03+0.05×2+0.07）×2×100=0.4×100=40（人）；…（4分）
（2）根据频率分布直方图得，样本的平均数是：

(55×0.01+57×0.03+59×0.05+61×0.05+63×0.07+65×0.08+67×0.06 +69×0.05+71×0.04+73×0.04+75×0.02)×2=65.2(kg)

利用平均数来衡量该地区17.5-18岁的男生体重是65.2kg；…（8分）
（3）根据频率分布直方图得，样本数据中低于62kg的频率是（0.01+0.03+0.05×2）×2=0.14，
∴这100名男生中随意抽取1人，该生体重低于62kg的概率是P=0.14．…（12分）

点评：本题考查了频率分布直方图的应用问题，解题时应利用频率分布直方图进行有关的计算，是基础题．