题目内容
| 2sin23°cos23°-sin16°cos30° |
| cos′16° |
A、-
| ||||
B、-
| ||||
C、
| ||||
D、
|
考点：两角和与差的正弦函数,三角函数的化简求值,二倍角的正弦
专题：三角函数的求值
分析：直接利用二倍角公式以及两角和的正弦函数化简求解即可．
解答：
解：
=
=
=
=sin30°
=
．
故选：C．
| 2sin23°cos23°-sin16°cos30° |
| cos′16° |
=
| sin46°-sin16°cos30° |
| cos′16° |
=
| sin(16°+30°)-sin16°cos30° |
| cos′16° |
=
| sin16°cos30°+cos16°sin30°-sin16°cos30° |
| cos′16° |
=sin30°
=
| 1 |
| 2 |
故选：C．
点评：本题考查三角函数的化简求值，两角和与差的三角函数以及二倍角公式的应用，考查计算能力
练习册系列答案
导学教程高中新课标系列答案
相关题目
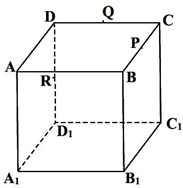如图，正方体ABCD-A1B1C1D1的棱长为2，P，Q，R分别是棱BC，CD，DD1的中点．下列命题：
如图，a，b是异面直线，画出平面α，使a?α，且b∥α，并说明理由．在△ABC中，AB=2，BC=1，∠ABC=60°．若使之绕直线BC旋转一周，则所形成的几何体的体积是（ ）
A、
| ||
| B、π | ||
| C、3π | ||
| D、9π |