题目内容
已知在△ABC中,A(1,0),B(0,-2),点C在抛物线y=x2上,求△ABC面积的最小值.
考点:抛物线的简单性质
专题:圆锥曲线的定义、性质与方程
分析:切点为(x0,x02),利用导数求出(1,1)再求出AB=
,点C到直线的距离最小d=
,利用面积公式即可.
| 5 |
| 1 | ||
|
| ||
| 5 |
解答:
解:∵A(1,0),B(0,-2),
∴AB方程为y=2x-2,AB=
,
∵抛物线y=x2上点C到直线的距离最小即可△ABC面积的最小值,
∴确定斜率为2的切线即可.
∵y=x2的导数:y′=2x,切点为(x0,x02),
2x0=2,x0=1,切点为C(1,1),
∴点C到直线的距离最小d=
,
∴△ABC面积的最小值为
×
×
=
,
故答案为:
.
∴AB方程为y=2x-2,AB=
| 5 |
∵抛物线y=x2上点C到直线的距离最小即可△ABC面积的最小值,
∴确定斜率为2的切线即可.
∵y=x2的导数:y′=2x,切点为(x0,x02),
2x0=2,x0=1,切点为C(1,1),
∴点C到直线的距离最小d=
| 1 | ||
|
| ||
| 5 |
∴△ABC面积的最小值为
| 1 |
| 2 |
| ||
| 5 |
| 5 |
| 1 |
| 2 |
故答案为:
| 1 |
| 2 |
点评:本题考查了抛物线的性质,导数的运用,属于综合题.

练习册系列答案
相关题目
设U为全集,A∩B=∅,则B∩(∁UA)为( )
| A、A | B、B |
| C、∁UB | D、∅ |
已知函数f(x)ax2+bx+c(x∈R,a>0)的零点为x1,x2(x1<x2),函数f(x)的最小值为y0,且y0∈[x1,x2],则函数y=f[f(x)]的零点个数是( )
| A、2或3 | B、3或4 | C、3 | D、4 |
在△ABC中,AB=2,BC=1,∠ABC=60°.若使之绕直线BC旋转一周,则所形成的几何体的体积是( )
A、
| ||
| B、π | ||
| C、3π | ||
| D、9π |
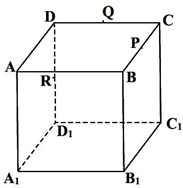 如图,正方体ABCD-A1B1C1D1的棱长为2,P,Q,R分别是棱BC,CD,DD1的中点.下列命题:
如图,正方体ABCD-A1B1C1D1的棱长为2,P,Q,R分别是棱BC,CD,DD1的中点.下列命题: 如图,a,b是异面直线,画出平面α,使a?α,且b∥α,并说明理由.
如图,a,b是异面直线,画出平面α,使a?α,且b∥α,并说明理由.