题目内容
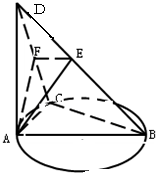 如图,AB为⊙O的直径,C为⊙O上一点,AD⊥平面ABC,AE⊥BD于E,AF⊥CD于F.求证:
如图,AB为⊙O的直径,C为⊙O上一点,AD⊥平面ABC,AE⊥BD于E,AF⊥CD于F.求证:(1)平面BCD⊥平面ACD;
(2)BD⊥平面AFE.
考点:平面与平面垂直的判定,直线与平面垂直的判定
专题:证明题,空间位置关系与距离
分析:(1)运用线面垂直的性质和判定,及直径所对的圆周角为直角,和面面垂直的判定定理,即可得证;
(2)运用线面垂直的性质和判定定理,即可得证.
(2)运用线面垂直的性质和判定定理,即可得证.
解答:
证明:(1)由于AD⊥平面ABC,则AD ⊥BC,
⊥BC,
由于AB为⊙O的直径,C为⊙O上一点,则BC⊥AC,
则有BC⊥平面ACD,
由于BC?平面BCD,则有平面BCD⊥平面ACD;
(2)由(1)得,BC⊥平面ACD,则BC⊥AF,
又AF⊥CD,则AF⊥平面BCD,
即有AF⊥BD,又AE⊥BD,
则有BD⊥平面AEF.
 ⊥BC,
⊥BC,由于AB为⊙O的直径,C为⊙O上一点,则BC⊥AC,
则有BC⊥平面ACD,
由于BC?平面BCD,则有平面BCD⊥平面ACD;
(2)由(1)得,BC⊥平面ACD,则BC⊥AF,
又AF⊥CD,则AF⊥平面BCD,
即有AF⊥BD,又AE⊥BD,
则有BD⊥平面AEF.
点评:本题考查线面垂直和面面垂直的性质和判定定理及运用,考查逻辑推理能力,属于中档题.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
已知集合M={m|(m-11)(m-16)≤0,m∈N},若(x3-
)n(n∈M)的二项展开式中存在常数项,则n等于( )
| 1 |
| x2 |
| A、16 | B、15 | C、14 | D、12 |
下列函数中,在定义域内是减函数的是( )
A、f(x)=-
| ||
B、f(x)=
| ||
| C、f(x)=2-x | ||
| D、f(x)=tanx |
 已知椭圆
已知椭圆 如图,在五棱锥P一ABCDE中,PA⊥平面ABCDE,AB∥CD,AC∥ED,AE∥BC,∠ABC=45°,AB=2
如图,在五棱锥P一ABCDE中,PA⊥平面ABCDE,AB∥CD,AC∥ED,AE∥BC,∠ABC=45°,AB=2