题目内容
已知g(x)=(x-a)2+(lnx-a)2,求证:g(x)≥
.
| 1 |
| 2 |
考点:导数在最大值、最小值问题中的应用
专题:证明题,导数的概念及应用,直线与圆
分析:g(x)=(x-a)2+(lnx-a)2,可看作是两点A(x,lnx)和B(a,a)的距离的平方,A在函数y=lnx上,B在直线y=x上,设直线y=x+t与函数y=lnx相切的一条直线,运用导数求出切点,求出切点到直线y=x的距离,即为A,B的最小值,再平方,即可得证.
解答:
证明:g(x)=(x-a)2+(lnx-a)2,
可看作是两点A(x,lnx)和B(a,a)的距离的平方,
A在函数y=lnx上,B在直线y=x上,
设直线y=x+t与函数y=lnx相切的一条直线,
可设切线为(m,n),则由(lnx)′=
,
即有切线斜率为
=1,解得m=1,n=0,
则切点为(1,0),切线为y=x-1,
此时切点到直线y=x的距离即为A,B两点距离的最小值,
即为
=
.
故g(x)≥(
)2=
.
可看作是两点A(x,lnx)和B(a,a)的距离的平方,
A在函数y=lnx上,B在直线y=x上,
设直线y=x+t与函数y=lnx相切的一条直线,
可设切线为(m,n),则由(lnx)′=
| 1 |
| x |
即有切线斜率为
| 1 |
| m |
则切点为(1,0),切线为y=x-1,
此时切点到直线y=x的距离即为A,B两点距离的最小值,
即为
| |1-0| | ||
|
| ||
| 2 |
故g(x)≥(
| ||
| 2 |
| 1 |
| 2 |
点评:本题考查导数的运用:求切线方程,考查两点的距离和点到直线的距离的公式及运用,考查运算能力,属于中档题.

练习册系列答案
相关题目
设a=
,b=log3
,c=log5
,则a,b,c之间的大小关系是( )
| 1 |
| 4 |
| 8 |
| 5 |
| 3 |
| A、a>b>c |
| B、b>c>a |
| C、c>a>b |
| D、c>b>a |
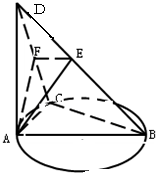 如图,AB为⊙O的直径,C为⊙O上一点,AD⊥平面ABC,AE⊥BD于E,AF⊥CD于F.求证:
如图,AB为⊙O的直径,C为⊙O上一点,AD⊥平面ABC,AE⊥BD于E,AF⊥CD于F.求证: