题目内容
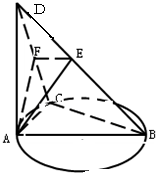
 如图,在五棱锥P一ABCDE中,PA⊥平面ABCDE,AB∥CD,AC∥ED,AE∥BC,∠ABC=45°,AB=2
如图,在五棱锥P一ABCDE中,PA⊥平面ABCDE,AB∥CD,AC∥ED,AE∥BC,∠ABC=45°,AB=2| 2 |
(1)求证:平面PCD⊥平面PAC
(2)求四棱锥P一ACDE的体积.
考点:棱柱、棱锥、棱台的体积,平面与平面垂直的判定
专题:空间位置关系与距离
分析:(1)要证平面PCD⊥平面PAC,只需证明平面PCD内的直线CD,垂直平面PAC内的两条相交直线PA、AC即可;
(2)直接求出底面面积和高,再求四棱锥P-ACDE的体积.
(2)直接求出底面面积和高,再求四棱锥P-ACDE的体积.
解答:
解:(1)证明:因为∠ABC=45°,AB=2
,BC=4,
所以在△ABC中,由余弦定理得:AC2=(2
)2+42-2×2
×4cos45°=8,解得AC=2
,
所以AB2+AC2=8+8=16=BC2,即AB⊥AC,
又PA⊥平面ABCDE,所以PA⊥AB,
又PA∩AC=A,所以AB⊥平面PAC,又AB∥CD,所以CD⊥平面PAC,
又因为CD?平面PCD,所以平面PCD⊥平面PAC;
(2)由(1)知CD⊥平面PAC,所以CD⊥AC,又AC∥ED,所以四边形ACDE是直角梯形,又容易求得DE=
,AC=2
,
所以四边形ACDE的面积为
(
+2
)×
=3,
所以四棱锥P-ACDE的体积为
×2
×3=2
| 2 |
所以在△ABC中,由余弦定理得:AC2=(2
| 2 |
| 2 |
| 2 |
所以AB2+AC2=8+8=16=BC2,即AB⊥AC,
又PA⊥平面ABCDE,所以PA⊥AB,
又PA∩AC=A,所以AB⊥平面PAC,又AB∥CD,所以CD⊥平面PAC,
又因为CD?平面PCD,所以平面PCD⊥平面PAC;
(2)由(1)知CD⊥平面PAC,所以CD⊥AC,又AC∥ED,所以四边形ACDE是直角梯形,又容易求得DE=
| 2 |
| 2 |
所以四边形ACDE的面积为
| 1 |
| 2 |
| 2 |
| 2 |
| 2 |
所以四棱锥P-ACDE的体积为
| 1 |
| 3 |
| 2 |
| 2 |
点评:本题主要考查空间中的基本关系,考查线面垂直、面面垂直的判定以及线面角和几何体体积的计算,考查识图能力、空间想象能力和逻辑推理能力.

练习册系列答案
相关题目
设a=
,b=log3
,c=log5
,则a,b,c之间的大小关系是( )
| 1 |
| 4 |
| 8 |
| 5 |
| 3 |
| A、a>b>c |
| B、b>c>a |
| C、c>a>b |
| D、c>b>a |
 如图,AB为⊙O的直径,C为⊙O上一点,AD⊥平面ABC,AE⊥BD于E,AF⊥CD于F.求证:
如图,AB为⊙O的直径,C为⊙O上一点,AD⊥平面ABC,AE⊥BD于E,AF⊥CD于F.求证: