题目内容
已知函数f(x)=ln(x+1)-ax(a∈R).
(Ⅰ)若a=1,求证:当x>0时,f(x)<0;
(Ⅱ)求函数f(x)的单调区间;
(Ⅲ)求证:(1+
)(1+
)…(1+
)<e.
(Ⅰ)若a=1,求证:当x>0时,f(x)<0;
(Ⅱ)求函数f(x)的单调区间;
(Ⅲ)求证:(1+
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2n |
考点:利用导数研究函数的单调性,利用导数求闭区间上函数的最值
专题:导数的综合应用
分析:(Ⅰ)利用导数判定函数的单调性,可得f(x)在(0,+∞)上单调递减,故f(x)<f(0)=0;
(Ⅱ)f′(x)=
-a=
,分a≥0和a<0,讨论可得函数的单调区间;
(Ⅲ)要证:(1+
)(1+
)…(1+
)<e,两边取以e为底的对数,即只需证明ln(1+
)+ln(1+
)+…+ln(1+
)<1,
由(Ⅰ)可知,ln(x+1)<x(x>0),分别取x=
,
,…,
,即可得出结论成立.
(Ⅱ)f′(x)=
| 1 |
| x+1 |
| (1-a)-ax |
| x+1 |
(Ⅲ)要证:(1+
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2n |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2n |
由(Ⅰ)可知,ln(x+1)<x(x>0),分别取x=
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2n |
解答:
(Ⅰ)证明:∵a=1,∴f(x)=ln(x+1)-x,
∴f′(x)=
-1=
,
∴当x>0时,f′(x)<0,f(x)在(0,+∞)上单调递减,
∴f(x)<f(0)=0.
(Ⅱ)解:∵f(x)=ln(x+1)-ax,∴f(x)的定义域为(-1,+∞),
∴f′(x)=
-a=
,
∴①当a≤0时,f′(x)≥0,f(x)在(-1,+∞)单调递增;
②当a>0时,x∈(-1,-1+
)上,f′(x)>0,x∈(-1+
,+∞),f′(x)<0,
∴f(x)在(-1,-1+
)单调递增,在(-1+
,+∞)单调递减,
(Ⅲ)证明:要证:(1+
)(1+
)…(1+
)<e,两边取以e为底的对数,即只需证明
ln(1+
)+ln(1+
)+…+ln(1+
)<1,
由(Ⅰ)可知,ln(x+1)<x(x>0),分别取x=
,
,…,
,得到
ln(1+
)<
,ln(1+
)<
,…,ln(1+
)<
,
将上述n个不等式相加,得
ln(1+
)+ln(1+
)+…+ln(1+
)<
+
+…+
=1-
<1.
从而结论成立.
∴f′(x)=
| 1 |
| x+1 |
| -x |
| x+1 |
∴当x>0时,f′(x)<0,f(x)在(0,+∞)上单调递减,
∴f(x)<f(0)=0.
(Ⅱ)解:∵f(x)=ln(x+1)-ax,∴f(x)的定义域为(-1,+∞),
∴f′(x)=
| 1 |
| x+1 |
| (1-a)-ax |
| x+1 |
∴①当a≤0时,f′(x)≥0,f(x)在(-1,+∞)单调递增;
②当a>0时,x∈(-1,-1+
| 1 |
| a |
| 1 |
| a |
∴f(x)在(-1,-1+
| 1 |
| a |
| 1 |
| a |
(Ⅲ)证明:要证:(1+
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2n |
ln(1+
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2n |
由(Ⅰ)可知,ln(x+1)<x(x>0),分别取x=
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2n |
ln(1+
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 2n |
| 1 |
| 2n |
将上述n个不等式相加,得
ln(1+
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2n |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2n |
| 1 |
| 2n |
从而结论成立.
点评:本题主要考查利用导数研究函数的单调性求函数的单调区间及函数最值等知识,考查学生等价转化思想及分类讨论思想的运用能力,综合性、逻辑性强,属于难题

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,已知梯形ABCD的对角线AC和BD相交于P点,OP的延长线交BC于G,两腰BA,CD的延长线交于O点,EF∥BC且EF过P点.证明:
如图,已知梯形ABCD的对角线AC和BD相交于P点,OP的延长线交BC于G,两腰BA,CD的延长线交于O点,EF∥BC且EF过P点.证明: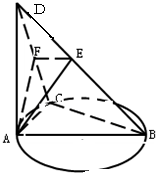 如图,AB为⊙O的直径,C为⊙O上一点,AD⊥平面ABC,AE⊥BD于E,AF⊥CD于F.求证:
如图,AB为⊙O的直径,C为⊙O上一点,AD⊥平面ABC,AE⊥BD于E,AF⊥CD于F.求证: