题目内容
下列函数中，在定义域内是减函数的是（ ）
A、f（x）=-
| ||
B、f（x）=
| ||
| C、f（x）=2-x | ||
| D、f（x）=tanx |
考点：函数单调性的判断与证明
专题：函数的性质及应用
分析：分别对A，B，C，D各个选项进行分析，从而得到答案．
解答：
解：对于A：f（x）=-
在（-∞，0）递增，在（0，+∞）递增，
对于B：f（x）=
在[0，+∞）递增，
对于C：f（x）=2-x在（-∞，-∞）递减，
对于D：f（x）=tanx在（kπ-
，kπ+
）递增，
故选：C．
| 1 |
| x |
对于B：f（x）=
| x |
对于C：f（x）=2-x在（-∞，-∞）递减，
对于D：f（x）=tanx在（kπ-
| π |
| 2 |
| π |
| 2 |
故选：C．
点评：本题考查了函数的单调性问题，是一道基础题．
练习册系列答案
名师指导期末冲刺卷系列答案
开心蛙口算题卡系列答案
相关题目
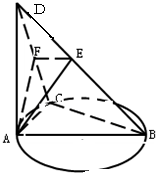如图，AB为⊙O的直径，C为⊙O上一点，AD⊥平面ABC，AE⊥BD于E，AF⊥CD于F．求证：若直线a⊥直线b，直线b⊥平面β，则a与β的关系是（ ）
| A、a⊥β | B、a∥β |
| C、a?β | D、a?β或a∥β |