题目内容
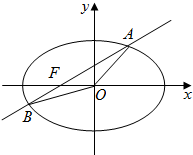 已知椭圆
已知椭圆| x2 |
| 2 |
(1)若直线l的倾斜角α=
| π |
| 4 |
(2)求弦AB的中点M的轨迹方程.
考点:轨迹方程,直线的倾斜角
专题:圆锥曲线的定义、性质与方程
分析:(1)直线方程与椭圆方程联立,利用弦长公式,即可求得结论;
(2)利用点差法,即可求弦AB的中点M的轨迹方程;
(2)利用点差法,即可求弦AB的中点M的轨迹方程;
解答:
解:(1)因为直线l的倾斜角α=
,直线l的斜率为1,方程为y=x+1,与椭圆方程联立,可得3x2+4x=0
设A(x1,y1),B(x2,y2),则x1=0,x2=-
∴|AB|=
|x1-x2|=
;
(2)当直线AB的斜率存在时
设弦AB的中点M的坐标为(x,y),A(x1,y1),B(x2,y2)
依题意有
,又
=
,化简可得x2+x+2y2=0.…(7分)
当直线AB的斜率不存在时,中点为F(-1,0)也满足上式.
综上得:弦AB的中点M的轨迹方程为x2+x+2y2=0.
| π |
| 4 |
设A(x1,y1),B(x2,y2),则x1=0,x2=-
| 4 |
| 3 |
∴|AB|=
| 2 |
4
| ||
| 3 |
(2)当直线AB的斜率存在时
设弦AB的中点M的坐标为(x,y),A(x1,y1),B(x2,y2)
依题意有
|
| y1-y2 |
| x1-x2 |
| -x |
| 2y |
当直线AB的斜率不存在时,中点为F(-1,0)也满足上式.
综上得:弦AB的中点M的轨迹方程为x2+x+2y2=0.
点评:本题考查直线与椭圆的位置关系中弦长的求法以及利用点差法求弦中点轨迹方程,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
若直线a⊥直线b,直线b⊥平面β,则a与β的关系是( )
| A、a⊥β | B、a∥β |
| C、a?β | D、a?β或a∥β |
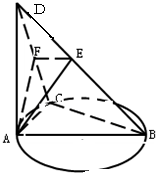 如图,AB为⊙O的直径,C为⊙O上一点,AD⊥平面ABC,AE⊥BD于E,AF⊥CD于F.求证:
如图,AB为⊙O的直径,C为⊙O上一点,AD⊥平面ABC,AE⊥BD于E,AF⊥CD于F.求证: