题目内容
已知集合M={m|(m-11)(m-16)≤0,m∈N},若(x3-
)n(n∈M)的二项展开式中存在常数项,则n等于( )
| 1 |
| x2 |
| A、16 | B、15 | C、14 | D、12 |
考点:二项式定理的应用
专题:计算题,集合,二项式定理
分析:化简集合M,求出二项式的通项公式,化简整理后,令x的指数为0,对照M中的元素,即可得到答案.
解答:
解:集合M={m|(m-11)(m-16)≤0,m∈N}={11,12,13,14,15,16},
(x3-
)n(n∈M)的二项展开式的通项公式为Tr+1=
(x3)n-r(-
)r
=
(-1)rx3n-5r,令3n-5r=0,则n=
,
由于n∈M,则n=15.
故选B.
(x3-
| 1 |
| x2 |
| C | r n |
| 1 |
| x2 |
=
| C | r n |
| 5r |
| 3 |
由于n∈M,则n=15.
故选B.
点评:本题考查二项式定理及运用,考查集合的化简和二项式的展开式的通项公式的运用,考查运算能力,属于基础题.

练习册系列答案
相关题目
若直线a⊥直线b,直线b⊥平面β,则a与β的关系是( )
| A、a⊥β | B、a∥β |
| C、a?β | D、a?β或a∥β |
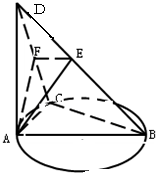 如图,AB为⊙O的直径,C为⊙O上一点,AD⊥平面ABC,AE⊥BD于E,AF⊥CD于F.求证:
如图,AB为⊙O的直径,C为⊙O上一点,AD⊥平面ABC,AE⊥BD于E,AF⊥CD于F.求证: