题目内容
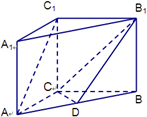 如图,在直三棱柱ABC-A1B1C1(侧棱与底面垂直的棱柱称为直棱柱)中,AC=CC1=3,BC=4,AB=5,点D是AB的中点.
如图,在直三棱柱ABC-A1B1C1(侧棱与底面垂直的棱柱称为直棱柱)中,AC=CC1=3,BC=4,AB=5,点D是AB的中点.(1)求证:AC1∥平面CDB1;
(2)求异面直线AC1与CB1所成的角的余弦值.
考点:异面直线及其所成的角,直线与平面平行的判定
专题:计算题,空间位置关系与距离,空间角
分析:(1)连接BC1,交CB1于E,连接DE,运用中位线定理,以及线面平行的判定定理,即可得证;
(2)由(1)可得DE∥AC1,DE=
AC1,则DE和直线CB1所成的角或补角即为异面直线AC1与CB1所成的角.
运用平面几何的知识,求出CD,CE,DE的长,再由余弦定理,即可得到.
(2)由(1)可得DE∥AC1,DE=
| 1 |
| 2 |
运用平面几何的知识,求出CD,CE,DE的长,再由余弦定理,即可得到.
解答:
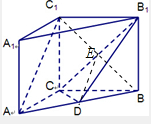 (1)证明:连接BC1,交CB1于E,连接DE,
(1)证明:连接BC1,交CB1于E,连接DE,
由于D为中点,E为中点,
则DE∥AC1,DE?平面CDB1,AC1?平面CDB1,
则有AC1∥平面CDB1;
(2)解:由(1)可得DE∥AC1,DE=
AC1,
则DE和CB1所成的角或补角即为异面直线AC1与CB1所成的角.
在三角形ABC中,AC=3,BC=4,AB=5,则△ABC为直角三角形,AB为斜边,
即有CD=
,AC1=
=3
,DE=
,CE=
CB1=
,
在三角形CDE中,cos∠CED=
=
.
故异面直线AC1与CB1所成的角的余弦值为
.
 (1)证明:连接BC1,交CB1于E,连接DE,
(1)证明:连接BC1,交CB1于E,连接DE,由于D为中点,E为中点,
则DE∥AC1,DE?平面CDB1,AC1?平面CDB1,
则有AC1∥平面CDB1;
(2)解:由(1)可得DE∥AC1,DE=
| 1 |
| 2 |
则DE和CB1所成的角或补角即为异面直线AC1与CB1所成的角.
在三角形ABC中,AC=3,BC=4,AB=5,则△ABC为直角三角形,AB为斜边,
即有CD=
| 5 |
| 2 |
| AC2+CC12 |
| 2 |
3
| ||
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |
在三角形CDE中,cos∠CED=
| ||||||
2×
|
3
| ||
| 10 |
故异面直线AC1与CB1所成的角的余弦值为
3
| ||
| 10 |
点评:本题考查直线与平面平行的判定定理,考查空间异面直线所成的角,考查运算能力和推理能力,属于基础题.

练习册系列答案
相关题目
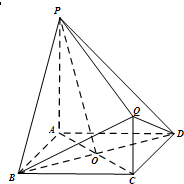 如图,PA,QC都与正方形ABCD所在平面垂直,AB=PA=2QC=2,AC∩BD=O
如图,PA,QC都与正方形ABCD所在平面垂直,AB=PA=2QC=2,AC∩BD=O
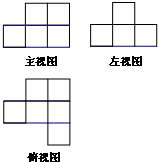 在一个仓库里堆积着正方体的货箱若干,要搬运这些箱子很困难,可是仓库管理员要清点一下箱子的数量,于是就想出一个办法:将这堆货物的三视图画了出来,你能根据三视图,帮他清点一下箱子的数量吗?这些正方体货箱的个数为( )
在一个仓库里堆积着正方体的货箱若干,要搬运这些箱子很困难,可是仓库管理员要清点一下箱子的数量,于是就想出一个办法:将这堆货物的三视图画了出来,你能根据三视图,帮他清点一下箱子的数量吗?这些正方体货箱的个数为( )