题目内容
以双曲线
-
=1的中心为顶点,求以该双曲线的右焦点为焦点的抛物线方程.
| x2 |
| 4 |
| y2 |
| 5 |
考点:双曲线的简单性质
专题:圆锥曲线的定义、性质与方程
分析:根据抛物线的方程,双曲线的方程,结合它的几何意义,求解抛物线的方程.
解答:
解:∵双曲线
-
=1,
∴中心为(0,0),a2=4,b2=5
该双曲线的右焦点为(3,0)
∴抛物线方程:y2=12x
| x2 |
| 4 |
| y2 |
| 5 |
∴中心为(0,0),a2=4,b2=5
该双曲线的右焦点为(3,0)
∴抛物线方程:y2=12x
点评:本题考查了双曲线,抛物线的几何意义,属于容易题.

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目
△ABC中,下面四个等式中不正确的是( )
| A、cos(A+B)=-cosC | ||||
| B、sin2(A+B)=sin2C | ||||
C、tan
| ||||
D、cos3(A+B)=1-2cos2
|
函数y=x2+2x的减区间是( )
| A、(-∞,-1] |
| B、[-1,+∞) |
| C、(-∞,0] |
| D、(-∞,+∞) |
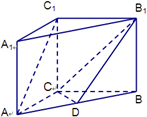 如图,在直三棱柱ABC-A1B1C1(侧棱与底面垂直的棱柱称为直棱柱)中,AC=CC1=3,BC=4,AB=5,点D是AB的中点.
如图,在直三棱柱ABC-A1B1C1(侧棱与底面垂直的棱柱称为直棱柱)中,AC=CC1=3,BC=4,AB=5,点D是AB的中点.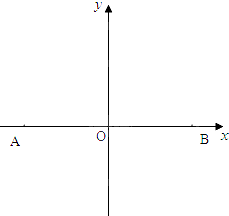 如图,A,B两地相距10km,A(-5,0),B(5,0).有一种商品,A、B两地均有出售且价格相同,某地居民从两地之一购得商品运回来,每公里的运费A地是B地的3倍.问该地居民应如何选择A地或B地购买此种商品最合算?(仅从运费的多少来考虑)
如图,A,B两地相距10km,A(-5,0),B(5,0).有一种商品,A、B两地均有出售且价格相同,某地居民从两地之一购得商品运回来,每公里的运费A地是B地的3倍.问该地居民应如何选择A地或B地购买此种商品最合算?(仅从运费的多少来考虑)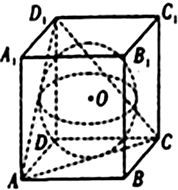 如图,已知球O是棱长为1的正方体ABCD-A1B1C1D1的内切球,则以B1为顶点,以球被平面ACD1截得的圆为底面的圆锥的全面积为
如图,已知球O是棱长为1的正方体ABCD-A1B1C1D1的内切球,则以B1为顶点,以球被平面ACD1截得的圆为底面的圆锥的全面积为