题目内容
已知函数f(x)=sin(
-ωx)(ω>0)任意两个零点之间的最小距离为
.
(Ⅰ)若f(α)=
,α∈[-π,π],求α的取值集合;
(Ⅱ)求函数y=f(x)-cos(ωx+
)的单调递增区间.
| π |
| 2 |
| π |
| 2 |
(Ⅰ)若f(α)=
| 1 |
| 2 |
(Ⅱ)求函数y=f(x)-cos(ωx+
| π |
| 3 |
考点:正弦函数的单调性
专题:三角函数的求值,三角函数的图像与性质
分析:(Ⅰ)首先根据任意两个零点之间的距离求出最小正周期,进一步确定α的集合.
(Ⅱ)通过三角恒等变换求出正弦型函数的解析式,进一步利用整体思想求单调区间.
(Ⅱ)通过三角恒等变换求出正弦型函数的解析式,进一步利用整体思想求单调区间.
解答:
解:(Ⅰ)因为f(x)=sin(
-ωx)=cosωx,任意两个零点之间的最小距离为
,
所以:f(x)的最小正周期为π,故T=
=π,
又ω>0,
故ω=2
由f(α)=
,得cos2α=
,
所以2α=2kπ±
,(k∈Z),
即α=kπ±
又α∈[-π,π],
所以α∈{-
,-
,
,
}.
(Ⅱ)函数 y=cos2x-cos(2x+
)=
cos2x+
sin2x=sin(2x+
)
令2kπ-
≤2x+
≤2kπ+
(k∈Z),
解得:kπ-
≤x≤kπ+
所以函数的单调递增区间为:[kπ-
,kπ+
](k∈Z).
| π |
| 2 |
| π |
| 2 |
所以:f(x)的最小正周期为π,故T=
| 2π |
| ω |
又ω>0,
故ω=2
由f(α)=
| 1 |
| 2 |
| 1 |
| 2 |
所以2α=2kπ±
| π |
| 3 |
即α=kπ±
| π |
| 6 |
又α∈[-π,π],
所以α∈{-
| 5π |
| 6 |
| π |
| 6 |
| π |
| 6 |
| 5π |
| 6 |
(Ⅱ)函数 y=cos2x-cos(2x+
| π |
| 3 |
| 1 |
| 2 |
| ||
| 2 |
| π |
| 6 |
令2kπ-
| π |
| 2 |
| π |
| 6 |
| π |
| 2 |
解得:kπ-
| π |
| 3 |
| π |
| 6 |
所以函数的单调递增区间为:[kπ-
| π |
| 3 |
| π |
| 6 |
点评:本题考查的知识要点:正弦函数的最小正周期的求法,正弦型函数的单调区间.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
函数y=x2+2x的减区间是( )
| A、(-∞,-1] |
| B、[-1,+∞) |
| C、(-∞,0] |
| D、(-∞,+∞) |
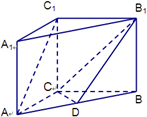 如图,在直三棱柱ABC-A1B1C1(侧棱与底面垂直的棱柱称为直棱柱)中,AC=CC1=3,BC=4,AB=5,点D是AB的中点.
如图,在直三棱柱ABC-A1B1C1(侧棱与底面垂直的棱柱称为直棱柱)中,AC=CC1=3,BC=4,AB=5,点D是AB的中点.