题目内容
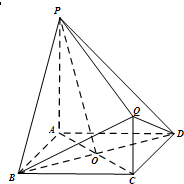 如图,PA,QC都与正方形ABCD所在平面垂直,AB=PA=2QC=2,AC∩BD=O
如图,PA,QC都与正方形ABCD所在平面垂直,AB=PA=2QC=2,AC∩BD=O(Ⅰ)求证:OP⊥平面QBD;
(Ⅱ)求二面角P-BQ-D平面角的余弦值;
(Ⅲ)过点C与平面PBQ平行的平面交PD于点E,求
| PE |
| ED |
考点:二面角的平面角及求法,直线与平面平行的判定
专题:空间位置关系与距离,空间角,空间向量及应用
分析:对第(1)问,要证OP⊥平面QBD,连结OQ,只需证OP⊥BD,OP⊥OQ,前者可由BD⊥平面PAO得证,后者可由△PAO∽△OCQ得证;
对第(2)问,以A为原点,分别以AB,AD,AP所在直线为x,y,z轴建立空间直角坐标系,分别求出平面PBQ与平面BDQ的法向量,通过两法向量的夹角探求二面角的大小;
对第(3)问,设
=λ
,用λ表示向量
的坐标,根据
与平面PBQ的法向量的垂直关系建立方程,即可得λ的值.
对第(2)问,以A为原点,分别以AB,AD,AP所在直线为x,y,z轴建立空间直角坐标系,分别求出平面PBQ与平面BDQ的法向量,通过两法向量的夹角探求二面角的大小;
对第(3)问,设
| PE |
| ED |
| CE |
| CE |
解答:
 (Ⅰ)证明:连接OQ,由题知PA∥QC,∴P、A、Q、C四点共面,易知BD⊥AC,BD⊥PA,又PA∩AC=A,
(Ⅰ)证明:连接OQ,由题知PA∥QC,∴P、A、Q、C四点共面,易知BD⊥AC,BD⊥PA,又PA∩AC=A,
∴BD⊥平面PACQ,得BD⊥OP.
由题中数据得PA=2,AO=OC=
,QC=1,∴
=
,△PAO∽△OCQ,∴∠POA=∠OQC,
又∵∠POA+∠OPA=90°,∴∠POA+∠COQ=90°,∴OP⊥OQ.
(或计算OQ=
,OP=
,PQ=3,由勾股定理得出∠POQ=90°,即OP⊥OQ)
∵BD∩OQ=O,∴OP⊥平面QBD.
(Ⅱ)解:如图右图所示,以A为原点,分别以AB,AD,AP所在直线为x,y,z轴建立空间直角坐标系,
由题意,得A(0,0,0),B(2,0,0),C(2,2,0),D(0,2,0),P(0,0,2),Q(2,2,1),O(1,1,0),
∴
=(-1,-1,2),
=(-2,0,2),
=(0,2,1),设平面PBQ的法向量为
=(x,y,z),
∴
,得
,不妨取y=-1,得
=(2,-1,2),
由(Ⅰ)知,
是平面BDQ的一个法向量,于是cos<
,
>=
=
,由图知,二面角P-BQ-D为锐二面角,
∴二面角P-BQ-D的平面角的余弦值为
.
(Ⅲ)解:设
=λ
,∴
=
+
=(1+λ)
=(0,2,-2),
=
(0,2,-2),
从而
=
+
=(-2,-
,
),
∵CE∥平面PBQ,∴
与平面PBQ的法向量
=(2,-1,2)垂直,则
•
=-4+
+
=0,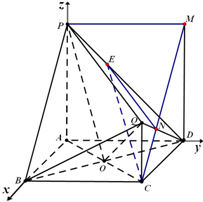
得λ=
,即
=
.
另解:在平面PAD中,分别过点D、P作直线PA、AD的平行线相交于点M,
连结MC交直线DQ与点N,在平面PQD中过点N作直线NE∥PQ交PQ于点E,如右图所示.
由题可知CN∥PB,NE∥PQ,CN∩NE=N,∴平面CNE∥平面PBQ,∴CE∥平面PBQ.
显然,△QCN∽△DMN,由CQ=1,MD=PA=2,∴
=
=
=
,即
=
.
 (Ⅰ)证明:连接OQ,由题知PA∥QC,∴P、A、Q、C四点共面,易知BD⊥AC,BD⊥PA,又PA∩AC=A,
(Ⅰ)证明:连接OQ,由题知PA∥QC,∴P、A、Q、C四点共面,易知BD⊥AC,BD⊥PA,又PA∩AC=A,∴BD⊥平面PACQ,得BD⊥OP.
由题中数据得PA=2,AO=OC=
| 2 |
| PA |
| OC |
| AO |
| QC |
又∵∠POA+∠OPA=90°,∴∠POA+∠COQ=90°,∴OP⊥OQ.
(或计算OQ=
| 3 |
| 6 |
∵BD∩OQ=O,∴OP⊥平面QBD.
(Ⅱ)解:如图右图所示,以A为原点,分别以AB,AD,AP所在直线为x,y,z轴建立空间直角坐标系,
由题意,得A(0,0,0),B(2,0,0),C(2,2,0),D(0,2,0),P(0,0,2),Q(2,2,1),O(1,1,0),
∴
| OP |
| BP |
| BQ |
| n |
∴
|
|
| n |
由(Ⅰ)知,
| OP |
| OP |
| n |
| ||||
|
|
| ||
| 6 |
∴二面角P-BQ-D的平面角的余弦值为
| ||
| 6 |
(Ⅲ)解:设
| PE |
| ED |
| PD |
| PE |
| ED |
| ED |
| ED |
| 1 |
| 1+λ |
从而
| CE |
| CD |
| DE |
| 2 |
| 1+λ |
| 2 |
| 1+λ |
∵CE∥平面PBQ,∴
| CE |
| n |
| n |
| CE |
| 2 |
| 1+λ |
| 4 |
| 1+λ |

得λ=
| 1 |
| 2 |
| PE |
| ED |
| 1 |
| 2 |
另解:在平面PAD中,分别过点D、P作直线PA、AD的平行线相交于点M,
连结MC交直线DQ与点N,在平面PQD中过点N作直线NE∥PQ交PQ于点E,如右图所示.
由题可知CN∥PB,NE∥PQ,CN∩NE=N,∴平面CNE∥平面PBQ,∴CE∥平面PBQ.
显然,△QCN∽△DMN,由CQ=1,MD=PA=2,∴
| PE |
| ED |
| QN |
| ND |
| QC |
| MD |
| 1 |
| 2 |
| PE |
| ED |
| 1 |
| 2 |
点评:本题主要考查空间直线与平面垂直的判断、线面平行的判断及二面角大小的计算、空间向量应用的基本方法,考查空间想象、计算、推理论证等能力,第(3)问的难度较大.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
下列四个命题中,错误的是( )
A、已知函数f(x)=
| ||
B、设回归直线方程为
| ||
| C、已知ξ服从正态分布 N(0,σ2),且P(-2≤ξ≤0)=0.4,则P(ξ>2)=0.1 | ||
| D、对于命题p:“?x∈R,x2+x+1<0”,则?p:“?x∈R,x2+x+1>0” |
现要完成下列3项抽样调查:
①从10盒酸奶中抽取3盒进行食品卫生检查;
②科技报告厅有32排作为,每排40个座位,有一次报告会恰好坐满了听众,报告会结束后,为了听取意见,邀请32名听众进行座谈;
③某中学高三年级有12个班,文科班4个,理科班8个,为了了解全校学生对知识的掌握情况,拟抽取一个容量为50的样本.
较为合理的抽样方法是( )
①从10盒酸奶中抽取3盒进行食品卫生检查;
②科技报告厅有32排作为,每排40个座位,有一次报告会恰好坐满了听众,报告会结束后,为了听取意见,邀请32名听众进行座谈;
③某中学高三年级有12个班,文科班4个,理科班8个,为了了解全校学生对知识的掌握情况,拟抽取一个容量为50的样本.
较为合理的抽样方法是( )
| A、①简单随机抽样,②系统抽样,③分层抽样 |
| B、①简单随机抽样,②分层抽样,③系统抽样 |
| C、①系统抽样,②简单随机抽样,③分层抽样 |
| D、①分层抽样,②系统抽样,③简单随机抽样 |
△ABC中,下面四个等式中不正确的是( )
| A、cos(A+B)=-cosC | ||||
| B、sin2(A+B)=sin2C | ||||
C、tan
| ||||
D、cos3(A+B)=1-2cos2
|
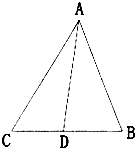 如图,在△ABC中,已知4sin2
如图,在△ABC中,已知4sin2 在锐角三角形ABC中,内角A,B,C的对边分别为a,b,c,且2b•sinA=
在锐角三角形ABC中,内角A,B,C的对边分别为a,b,c,且2b•sinA=
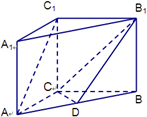 如图,在直三棱柱ABC-A1B1C1(侧棱与底面垂直的棱柱称为直棱柱)中,AC=CC1=3,BC=4,AB=5,点D是AB的中点.
如图,在直三棱柱ABC-A1B1C1(侧棱与底面垂直的棱柱称为直棱柱)中,AC=CC1=3,BC=4,AB=5,点D是AB的中点.