题目内容
圆心在x轴上、半径为
的圆C位于y轴左侧，且与直线x+2y=0相切，则圆C的标准方程是 ．
| 5 |
考点：圆的标准方程
专题：直线与圆
分析：由圆心到切线x+2y=0距离等于半径，得|a|=5，由位于y轴左侧得a=-5，由此能求出圆C的标准方程．
解答：
解：圆心在x轴上，是（a，0），r=
，
圆心到切线x+2y=0距离等于半径
所以
=
，
|a|=5
位于y轴左侧则a＜0
所以a=-5
圆C的标准方程为：（x+5）2+y2=5．
故答案为：（x+5）2+y2=5．
| 5 |
圆心到切线x+2y=0距离等于半径
所以
| |a+0| | ||
|
| 5 |
|a|=5
位于y轴左侧则a＜0
所以a=-5
圆C的标准方程为：（x+5）2+y2=5．
故答案为：（x+5）2+y2=5．
点评：本题考查圆的标准方程的求法，是基础题，解题时要认真审题，注意点到直线的距离公式的合理运用．
练习册系列答案
相关题目
若不等式组
表示的平面区域是一个三角形，则a的取值范围是（ ）
|
| A、[0，3] |
| B、[0，3） |
| C、[3，6） |
| D、[3，6] |
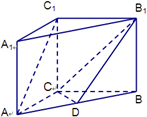如图，在直三棱柱ABC-A1B1C1（侧棱与底面垂直的棱柱称为直棱柱）中，AC=CC1=3，BC=4，AB=5，点D是AB的中点．
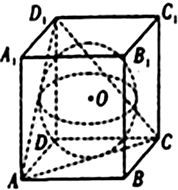如图，已知球O是棱长为1的正方体ABCD-A1B1C1D1的内切球，则以B1为顶点，以球被平面ACD1截得的圆为底面的圆锥的全面积为