题目内容
设椭圆C：
+
=1（a＞b＞0），F是它的左焦点，Q是右准线与x轴的交点，点P（0，3）满足
•
=0，N是直线PQ与椭圆的一个公共点，当|PN|：|NQ|=1：8时，求椭圆的方程．
| x2 |
| a2 |
| y2 |
| b2 |
| PF |
| PQ |
考点：抛物线的简单性质
专题：计算题,圆锥曲线的定义、性质与方程
分析：根据点P（0，3）满足
•
=0，利用数量积公式，可求a，结合|PN|：|NQ|=1：8，求出N的坐标，代入椭圆方程，即可求出椭圆的方程．
| PF |
| PQ |
解答：
解：∵点P（0，3）满足
•
=0，
∴（c，-3）•（-
，-3）=0，
∴-a2+9=0，
∴a=3，
∵P（0，3）、Q（-
，0），|PN|：|NQ|=1：8，
∴N（-
，
）．
把N点坐标代入椭圆方程，得：c=1．b2=8．
∴椭圆方程是：
+
=1．
| PF |
| PQ |
∴（c，-3）•（-
| a2 |
| c |
∴-a2+9=0，
∴a=3，
∵P（0，3）、Q（-
| 9 |
| c |
∴N（-
| 1 |
| c |
| 8 |
| 3 |
把N点坐标代入椭圆方程，得：c=1．b2=8．
∴椭圆方程是：
| x2 |
| 9 |
| y2 |
| 8 |
点评：本题考查椭圆的标准方程，考查向量知识的运用，考查学生的计算能力，确定N的坐标是关键．
练习册系列答案
相关题目
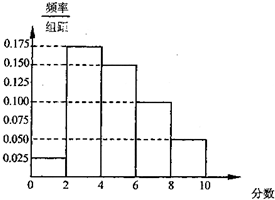某个团购网站为了更好地满足消费者需求，对在其网站发布的团购产品展开了用户调查，每个用户在使用了团购产品后可以对该产品进行打分，最高分是10分．上个月该网站共卖出了100份团购产品，所有用户打分的平均分作为该产品的参考分值，将这些产品按照得分分成以下几组：第一组[0，2），第二组[2，4），第三组[4，6），第四组[6，8），第五组[8，10]，得到的频率分布直方图如图所示．