Question

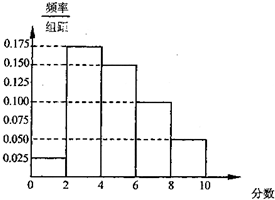某个团购网站为了更好地满足消费者需求，对在其网站发布的团购产品展开了用户调查，每个用户在使用了团购产品后可以对该产品进行打分，最高分是10分．上个月该网站共卖出了100份团购产品，所有用户打分的平均分作为该产品的参考分值，将这些产品按照得分分成以下几组：第一组[0，2），第二组[2，4），第三组[4，6），第四组[6，8），第五组[8，10]，得到的频率分布直方图如图所示．
（Ⅰ）分别求第三，四，五组的频率；
（Ⅱ）该网站在得分较高的第三，四，五组中用分层抽样的方法抽取6个产品．
①已知甲产品和乙产品均在第三组，求甲、乙同时被选中的概率；
②某人决定在这6个产品中随机抽取2个购买，设第4组中有X个产品被购买，求X的分布列和数学期望．

Answer 1

考点：离散型随机变量的期望与方差,分层抽样方法,频率分布直方图,古典概型及其概率计算公式

专题：概率与统计

分析：（Ⅰ）利用频率分布直方图能分别求出第三，四，五组的频率．
（Ⅱ）①由题意可知，在分层抽样的过程中第三组应抽到=3个，而第三组共有30个，由此能求出甲乙两产品同时被选中的概率．
②第四组共有X个产品被购买，由题意知X的取值为0，1，2，分别求出P（X=0），P（X=1），P（x=2），由此能求出X的分布列和数学期望．

解答： （Ⅰ）解：第三组的频率是0.150×2=0.3，
第四组的频率是0.100×2=0.2，
第五组的频率是0.050×2=0.1．…（3分）
（Ⅱ）①由题意可知，在分层抽样的过程中第三组应抽到6×0.5=3个，
而第三组共有100×0.3=30个，
∴甲乙两产品同时被选中的概率为p=

C 1 28

C 3 30

=

1

145

．…（7分）
②第四组共有X个产品被购买，∴X的取值为0，1，2，
P（X=0）=

C 1 3 +C 2 3

C 2 6

=

6

15

，
P（X=1）=

C 1 3 C 1 2 +C 1 2

C 2 6

=

8

15

，
P（x=2）=

C 2 2

C 2 6

=

1

15

，
∴X的分布列为：

X	0	1	2
P	2 5	8 15	1 15

…（10分）
EX=0×

2

5

+1×

8

15

+2×

1

15

=

2

3

．…（12分）

点评：本题考查频率分布直方图的应用，考查离散型随机变量的分布列和数学期望的求法，是中档题，解题时要认真审题，注意排列组合的合理运用．