题目内容
把函数y=sinx的图象上的每一点都沿着向量(
,-
)的方向移动
个单位,所得点的轨迹方程是 .
| π |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| π2+4 |
考点:函数y=Asin(ωx+φ)的图象变换
专题:计算题,三角函数的图像与性质,平面向量及应用
分析:向x轴正方向移动
个单位,向y轴正方向移动-
个单位,相当于沿着向量(
,-
)的方向移动了
=
×
,则有原题的移动即为向x轴正方向移动
个单位,向y轴正方向移动-1个单位.
即可得到轨迹方程.
| π |
| 4 |
| 1 |
| 2 |
| π |
| 4 |
| 1 |
| 2 |
(
|
| 1 |
| 2 |
| ||
| 2 |
| π |
| 2 |
即可得到轨迹方程.
解答:
解:向x轴正方向移动
个单位,向y轴正方向移动-
个单位,
相当于沿着向量(
,-
)的方向移动了
=
×
,
则有原题的移动即为向x轴正方向移动
×2=
个单位,向y轴正方向移动-
×2=-1个单位.
故得轨迹方程y=sin(x-
)-1,
即为y=-cosx-1.
故答案为:y=-cosx-1.
| π |
| 4 |
| 1 |
| 2 |
相当于沿着向量(
| π |
| 4 |
| 1 |
| 2 |
(
|
| 1 |
| 2 |
| ||
| 2 |
则有原题的移动即为向x轴正方向移动
| π |
| 4 |
| π |
| 2 |
| 1 |
| 2 |
故得轨迹方程y=sin(x-
| π |
| 2 |
即为y=-cosx-1.
故答案为:y=-cosx-1.
点评:本题考查三角函数的图象平移,考查平面向量的运用,考查运算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知x,y满足不等式组
,则Z=x+2y的最小值为( )
|
| A、2 | B、3 | C、4 | D、-6 |
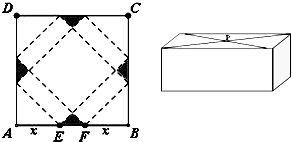
 在底面边长为2,高为1的正四梭柱ABCD-A1B1C1D1中,E,F分别为BC,C1D1的中点.则异面直线A1E,CF所成的角为
在底面边长为2,高为1的正四梭柱ABCD-A1B1C1D1中,E,F分别为BC,C1D1的中点.则异面直线A1E,CF所成的角为