题目内容
 在底面边长为2,高为1的正四梭柱ABCD-A1B1C1D1中,E,F分别为BC,C1D1的中点.则异面直线A1E,CF所成的角为
在底面边长为2,高为1的正四梭柱ABCD-A1B1C1D1中,E,F分别为BC,C1D1的中点.则异面直线A1E,CF所成的角为考点:异面直线及其所成的角
专题:计算题,空间角
分析:以D为原点建立空间直角坐标系,求出各点坐标,进而求出异面直线A1E,CF的方向向量,代入向量夹角公式,可得求异面直线A1E,CF所成的角.
解答:
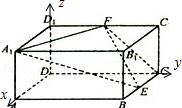 解:以D为原点建立空间直角坐标系,则A1(2,0,1),E(1,2,0),C(0,2,0),F(0,1,1),
解:以D为原点建立空间直角坐标系,则A1(2,0,1),E(1,2,0),C(0,2,0),F(0,1,1),
∴
=(-1,2,-1),
=(0,-1,1),
设异面直线A1E,CF所成的角为θ,
则cosθ=
=
,
所以θ=
,所求异面直线的夹角为
.
故答案为:
.
 解:以D为原点建立空间直角坐标系,则A1(2,0,1),E(1,2,0),C(0,2,0),F(0,1,1),
解:以D为原点建立空间直角坐标系,则A1(2,0,1),E(1,2,0),C(0,2,0),F(0,1,1),∴
| A1E |
| CF |
设异面直线A1E,CF所成的角为θ,
则cosθ=
| 3 | ||||
|
| ||
| 2 |
所以θ=
| π |
| 6 |
| π |
| 6 |
故答案为:
| π |
| 6 |
点评:本题考查异面直线及其所成的角,建立空间坐标系,将空间异面直线夹角问题转化为向量夹角问题是解答的关键.

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案
相关题目
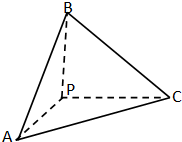 三棱锥P-ABC中,三侧棱PA,PB,PC两两互相垂直,且三角形△PAB,△PAC,△PBC的面积依次为1,1,2,则此三棱锥 P-ABC外接球的表面积为( )
三棱锥P-ABC中,三侧棱PA,PB,PC两两互相垂直,且三角形△PAB,△PAC,△PBC的面积依次为1,1,2,则此三棱锥 P-ABC外接球的表面积为( )| A、9π | B、12π |
| C、18π | D、36π |
设a=ln2,b=(ln2)2,c=ln
,则( )
| 2 |
| A、a>b>c |
| B、a>c>b |
| C、c>a>b |
| D、c>b>a |
下列命题正确的是( )
| A、经过三点,有且只有一个平面 |
| B、平行于同一条直线的两个平面的平行 |
| C、经过平面外一点有且只有一条直线与已知平面平行 |
| D、过一点有且只有一条直线垂直于已知平面 |