题目内容

2．已知zi=2-i，则复数z在复平面对应点的坐标是（　　）
A．（-1，-2）B．（-1，2）C．（1，-2）D．（1，2）

分析 由题意可得z=$\frac{2-i}{i}$，再利用两个复数代数形式的乘除法法则化为a+bi的形式，从而求得z对应的点的坐标．

解答 解：zi=2-i，
∴z=$\frac{2-i}{i}$=$\frac{（2-i）i}{{i}^{2}}$=-1-2i，
∴复数z在复平面对应点的坐标是（-1，-2），
故选：A．

点评 本题主要考查两个复数代数形式的乘除法，虚数单位i的幂运算性质，复数与复平面内对应点之间的关系，属于基础题．

练习册系列答案
相关题目
18．已知数列{an}中，a1=2，且$\frac{{a_{n+1}^2}}{a_n}=4（{a_{n+1}}-{a_n}）（n∈{N^*}）$，则其前9项的和S9=1022．
13．命题p：?x∈R，tanx＞1，命题q：抛物线y=$\frac{1}{3}$x2的焦点到准线的距离为$\frac{1}{6}$，那么下列命题为真命题的是（　　）
A．￢pB．（￢p）∨qC．p∧qD．p∧（￢q）
10．已知集合A={（x，y）|x+y-1=0，x，y∈R}，B={（x，y）|y=x2+1，x，y∈R}，则集合A∩B的元素个数是（　　）
A．0B．1C．2D．3
17．已知点P是曲线C：xy=1（x＞0）上的点，Q是点P关于直线l：y=2x的对称点，R为直线l与曲线C的交点，则$\overrightarrow{OR}$•$\overrightarrow{OQ}$的最小值为（　　）
A．$\sqrt{3}$B．1C．$\sqrt{2}$D．2
7．定义上凸函数如下：设f（x）为区间I上的函数，若对任意的x1，x2∈I总有f（$\frac{{x}_{1}+{x}_{2}}{2}$）≤$\frac{f（{x}_{1}）+f（{x}_{2}）}{2}$，则称f（x）为I上的上凸函数，某同学查阅资料后发现了上凸函数有如下判定定理和性质定理：
判定定理：f（x）为上凸函数的充要条件是f″（x）≥0，x∈I，其中f″（x）为f（x）的导函数f′（x）的导数．
性质定理：若函数f（x）为区间I上的下凸函数，则对I内任意的x1，x2，…，xn，都有$\frac{f（{x}_{1}）+f（{x}_{2}）+…+f（{x}_{n}）}{n}$≥f（$\frac{{x}_{1}+{x}_{2}+…+{x}_{n}}{n}$）．
请问：在△ABC中，sinA+sinB+sinC的最大值为$\frac{3\sqrt{3}}{2}$．
14．如图，己知四棱锥P-ABCD的底面为矩形，PA⊥底面ABCD，且AB=$\sqrt{2}$，BC=1，点E，F分别为AB，PC中点．
（1）当PA的长度为多少时，EF⊥PD；
（2）在（1）的前提下，求：平面BPC与平面DPC的夹角余弦值．
11．在空间，可以确定一个平面的条件是（　　）
A．两条直线B．一点和一条直线C．三个点D．一个三角形
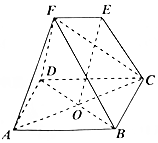12．如图，在几何体中，四边形ABCD为菱形，对角线AC与BD的交点为O，四边形DCEF为梯形，EF∥DC，FD=FB．
（Ⅰ）若DC=2EF，求证：OE∥平面ADF；
（Ⅱ）求证：平面AFC⊥平面ABCD；
（Ⅲ）若AB=FB=2，AF=3，∠BCD=60°，求AF与平面ABCD所成角．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网