题目内容
10．已知集合A={（x，y）|x+y-1=0，x，y∈R}，B={（x，y）|y=x2+1，x，y∈R}，则集合A∩B的元素个数是（ ）| A． | 0 | B． | 1 | C． | 2 | D． | 3 |
分析 A∩B={（x，y）|$\left\{\begin{array}{l}{x+y-1=0}\\{y={x}^{2}+1}\end{array}\right.$}，由此能求出A∩B中元素个数．
解答 解：∵集合A={（x，y）|x+y-1=0，x，y∈R}，
B={（x，y）|y=x2+1，x，y∈R}，
∴A∩B={（x，y）|$\left\{\begin{array}{l}{x+y-1=0}\\{y={x}^{2}+1}\end{array}\right.$}={（0，1），（-1，2）}，
集合A∩B的元素个数是2个．
故选：C．
点评 本题考查集合中元素个数的求法，是基础题，解题时要认真审题，注意交集性质的合理运用．
练习册系列答案
阅读快车系列答案
相关题目
6．
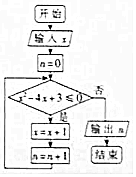执行如图所示的程序框图，若输入x的值为1，输出n的值为N，则在区间[-1，4]上随机选取一个数M，M≥N-1的概率为（ ）
执行如图所示的程序框图，若输入x的值为1，输出n的值为N，则在区间[-1，4]上随机选取一个数M，M≥N-1的概率为（ ）| A． | $\frac{1}{5}$ | B． | $\frac{2}{5}$ | C． | $\frac{3}{5}$ | D． | $\frac{4}{5}$ |
2．已知zi=2-i，则复数z在复平面对应点的坐标是（ ）
| A． | （-1，-2） | B． | （-1，2） | C． | （1，-2） | D． | （1，2） |
19．若实数x，y∈R，则“x＞0，y＞0”是“xy＞0”的（ ）
| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充要条件 | D． | 既不充分也不必要条件 |