题目内容
12.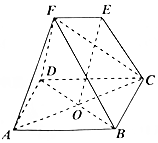 如图,在几何体中,四边形ABCD为菱形,对角线AC与BD的交点为O,四边形DCEF为梯形,EF∥DC,FD=FB.
如图,在几何体中,四边形ABCD为菱形,对角线AC与BD的交点为O,四边形DCEF为梯形,EF∥DC,FD=FB.(Ⅰ)若DC=2EF,求证:OE∥平面ADF;
(Ⅱ)求证:平面AFC⊥平面ABCD;
(Ⅲ)若AB=FB=2,AF=3,∠BCD=60°,求AF与平面ABCD所成角.
分析 (Ⅰ)取AD的中点G,连接OG,FG,证明OGFE为平行四边形,可得OE∥FG,即可证明:OE∥平面ADF;
(Ⅱ)证明BD⊥平面AFC,即可证明:平面AFC⊥平面ABCD;
(Ⅲ)做FH⊥AC于H,∠FAH为AF与平面ABCD所成角,即可求AF与平面ABCD所成角.
解答  (Ⅰ)证明:取AD的中点G,连接OG,FG.
(Ⅰ)证明:取AD的中点G,连接OG,FG.
∵对角线AC与BD的交点为O,
∴OG∥DC,OG=$\frac{1}{2}DC$,
∵EF∥DC,DC=2EF,
∴OG∥EF,OG=EF,
∴OGFE为平行四边形,
∴OE∥FG,
∵FG?平面ADF,OE?平面ADF,
∴OE∥平面ADF;
(Ⅱ)证明:∵四边形ABCD为菱形,
∴OC⊥BD,
∵FD=FB,O是BD的中点,
∴OF⊥BD,
∵OF∩OC=O,
∴BD⊥平面AFC,
∵?P?平面ABCD,
∴平面AFC⊥平面ABCD;
(Ⅲ)解:作FH⊥AC于H.
∵平面AFC⊥平面ABCD,∴FH⊥平面ABCD,
∴∠FAH为AF与平面ABCD所成角,
由题意,△BCD为正三角形,OA=$\sqrt{3}$,BD=AB=2,
∵FD=FB=2,
∴△FBD为正三角形,∴OF=$\sqrt{3}$.
△AOF中,由余弦定理可得cos∠AOF=$\frac{3+3-9}{2•\sqrt{3}•\sqrt{3}}$=-$\frac{1}{2}$,
∴∠AOF=120°,
∴∠FAH=∠FAO=30°,
∴AF与平面ABCD所成角为30°.
点评 本题考查线面平行,面面垂直的证明,考查线面角,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目
2.已知zi=2-i,则复数z在复平面对应点的坐标是( )
| A. | (-1,-2) | B. | (-1,2) | C. | (1,-2) | D. | (1,2) |
7.已知p:|x-1|<2,q:f(x)=$\frac{{x}^{2}+1}{x}$的最小值为2,则p是q的( )
| A. | 充分而不必要条件 | B. | 充要条件 | ||
| C. | 必要而不充分条件 | D. | 既不充分也不必要条件 |
2.已知集合A={0,1,2,3,4},B={x|x2-2x>0},则A∩B=( )
| A. | (2,4] | B. | [2,4] | C. | {0,3,4} | D. | {3,4} |
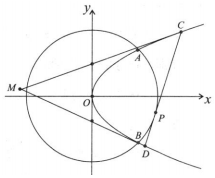 如图,抛物线E:y2=2px(p>0)与圆O:x2+y2=8相交于A,B两点,且点A的横坐标为2.过劣弧AB上动点P(x0,y0)作圆O的切线交抛物线E于C,D两点,分别以C,D为切点作抛物线E的切线l1,l2,l1与l2相交于点M.
如图,抛物线E:y2=2px(p>0)与圆O:x2+y2=8相交于A,B两点,且点A的横坐标为2.过劣弧AB上动点P(x0,y0)作圆O的切线交抛物线E于C,D两点,分别以C,D为切点作抛物线E的切线l1,l2,l1与l2相交于点M.