题目内容
14. 如图,己知四棱锥P-ABCD的底面为矩形,PA⊥底面ABCD,且AB=$\sqrt{2}$,BC=1,点E,F分别为AB,PC中点.
如图,己知四棱锥P-ABCD的底面为矩形,PA⊥底面ABCD,且AB=$\sqrt{2}$,BC=1,点E,F分别为AB,PC中点.(1)当PA的长度为多少时,EF⊥PD;
(2)在(1)的前提下,求:平面BPC与平面DPC的夹角余弦值.
分析 (1)以A为原点,建立如图所示的空间直角坐标系,设PA=x,
则P(0,0,x),D(-1,0,0),E(0,$\frac{\sqrt{2}}{2}$,0),C(-1,$\sqrt{2}$,0),F(-$\frac{1}{2}$,$\frac{\sqrt{2}}{2}$,$\frac{x}{2}$),$\overrightarrow{EF}•\overrightarrow{PD}=\frac{1}{2}+0-\frac{{x}^{2}}{2}=0$,得x.
(2)求出平面PBC、平面PDC的法向量.利用向量的夹角公式求解.
解答 解:(1)以A为原点,建立如图所示的空间直角坐标系,设PA=x,
则P(0,0,x),D(-1,0,0),E(0,$\frac{\sqrt{2}}{2}$,0),C(-1,$\sqrt{2}$,0),F(-$\frac{1}{2}$,$\frac{\sqrt{2}}{2}$,$\frac{x}{2}$),
又$\overrightarrow{EF}=(-\frac{1}{2},0,\frac{x}{2})$,$\overrightarrow{PD}=(-1,0,-x)$,
∵EF⊥PD,∴$\overrightarrow{EF}•\overrightarrow{PD}=\frac{1}{2}+0-\frac{{x}^{2}}{2}=0$,解得x=1.
∴当PA的长度为1时,EF⊥PD.
(2)由(1)可得$\overrightarrow{PB}=(0,\sqrt{2},-1),\overrightarrow{PC}=(-1,\sqrt{2},-1)$,$\overrightarrow{PD}=(-1,0,0)$,
设平面PBC的法向量为$\overrightarrow{m}=(x,y,z)$,$\left\{\begin{array}{l}{\overrightarrow{m}•\overrightarrow{PB}=\sqrt{2}y-z=0}\\{\overrightarrow{m}•\overrightarrow{PC}=-x+\sqrt{2}y-z=0}\end{array}\right.$,取$\overrightarrow{m}=(0,1,\sqrt{2})$.
同理可得平面PDC的法向量为$\overrightarrow{n}=(1,0,-1)$.
|cos<$\overrightarrow{m},\overrightarrow{n}$>|=$\frac{\sqrt{3}}{3}$,∴平面BPC与平面DPC的夹角余弦值$\frac{\sqrt{3}}{3}$.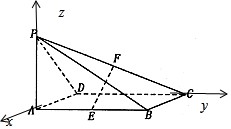
点评 本题考查了向量在处理动点问题中的应用,及向量法求二面角,属于中档题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | (-1,-2) | B. | (-1,2) | C. | (1,-2) | D. | (1,2) |
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |