题目内容
18．已知数列{an}中，a1=2，且$\frac{{a_{n+1}^2}}{a_n}=4（{a_{n+1}}-{a_n}）（n∈{N^*}）$，则其前9项的和S9=1022．分析 由题意整理可得：an+1=2an，则数列{an}以2为首项，以2为公比的等比数列，利用等比数列的前n项和公式，即可求得S9．
解答 解：由题意可知an+12=4an（an+1-an），
则an+12=4（anan+1-an2），an+12-4anan+1+4an2=0
整理得：（an+1-2an）2=0，则an+1=2an，
∴数列{an}以2为首项，以2为公比的等比数列，
则前9项的和S9=$\frac{{a}_{1}（1-{q}^{n}）}{1-q}$=$\frac{2（1-{2}^{9}）}{1-2}$=1022，
故答案为：1022．
点评 本题考查等比数列的性质，考查等比数列的前n项和公式，考查计算能力，属于中档题．
练习册系列答案
相关题目
9．已知函数f（x）=$\left\{\begin{array}{l}{（\frac{1}{2}）^{x}，x≥3}\\{f（x+1），x＜3}\end{array}\right.$f（log23）的值为（ ）
| A． | $\frac{1}{3}$ | B． | $\frac{1}{6}$ | C． | $\frac{1}{12}$ | D． | $\frac{1}{24}$ |
6．
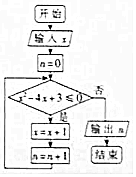执行如图所示的程序框图，若输入x的值为1，输出n的值为N，则在区间[-1，4]上随机选取一个数M，M≥N-1的概率为（ ）
执行如图所示的程序框图，若输入x的值为1，输出n的值为N，则在区间[-1，4]上随机选取一个数M，M≥N-1的概率为（ ）| A． | $\frac{1}{5}$ | B． | $\frac{2}{5}$ | C． | $\frac{3}{5}$ | D． | $\frac{4}{5}$ |
13．已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1（a＞b＞0）的左，右焦点为F1，F2，离心率为e．P是椭圆上一点，满足PF2⊥F1F2，点Q在线段PF1上，且$\overrightarrow{{F_1}Q}=2\overrightarrow{QP}$．若$\overrightarrow{{F_1}P}•\overrightarrow{{F_2}Q}$=0，则e2=（ ）
| A． | $\sqrt{2}-1$ | B． | $2-\sqrt{2}$ | C． | $2-\sqrt{3}$ | D． | $\sqrt{5}-2$ |
2．已知zi=2-i，则复数z在复平面对应点的坐标是（ ）
| A． | （-1，-2） | B． | （-1，2） | C． | （1，-2） | D． | （1，2） |