题目内容
7.定义上凸函数如下:设f(x)为区间I上的函数,若对任意的x1,x2∈I总有f($\frac{{x}_{1}+{x}_{2}}{2}$)≤$\frac{f({x}_{1})+f({x}_{2})}{2}$,则称f(x)为I上的上凸函数,某同学查阅资料后发现了上凸函数有如下判定定理和性质定理:判定定理:f(x)为上凸函数的充要条件是f″(x)≥0,x∈I,其中f″(x)为f(x)的导函数f′(x)的导数.
性质定理:若函数f(x)为区间I上的下凸函数,则对I内任意的x1,x2,…,xn,都有$\frac{f({x}_{1})+f({x}_{2})+…+f({x}_{n})}{n}$≥f($\frac{{x}_{1}+{x}_{2}+…+{x}_{n}}{n}$).
请问:在△ABC中,sinA+sinB+sinC的最大值为$\frac{3\sqrt{3}}{2}$.
分析 构造函数f(x)=sinx,x∈(0,π),求导,则f″(x)≤-sinx,由正弦函数的图象可知f″(x)<0成立,则f(x)=sinx,x∈(0,π)是凸函数,根据凸函数的性质sinA+sinB+sinC≤3sin($\frac{A+B+C}{3}$),即可求得sinA+sinB+sinC的最大值.
解答 解:设f(x)=sinx,x∈(0,π),则f′(x)=cosx,则f″(x)≤-sinx,x∈(0,π),
由当x∈(0,π),0<sin≤1,则f″(x)<0成立,则f(x)=sinx,x∈(0,π)是凸函数,
由凸函数的性质可知:$\frac{f({x}_{1})+f({x}_{2})+…+f({x}_{n})}{n}$≤f($\frac{{x}_{1}+{x}_{2}+…+{x}_{n}}{n}$).
则sinA+sinB+sinC≤3sin($\frac{A+B+C}{3}$)=3×sin$\frac{π}{3}$=$\frac{3\sqrt{3}}{2}$,
∴sinA+sinB+sinC的最大值为$\frac{3\sqrt{3}}{2}$,
故答案为:$\frac{3\sqrt{3}}{2}$.
点评 本题考查凸函数的性质,考查正弦函数的性质,考查转化思想,属于中档题.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
2.已知zi=2-i,则复数z在复平面对应点的坐标是( )
| A. | (-1,-2) | B. | (-1,2) | C. | (1,-2) | D. | (1,2) |
12.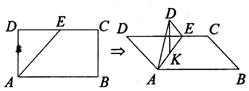 如图在矩形ABCD中,AB=2$\sqrt{3}$,BC=2,E为线段DC上一动点,现将△AED沿AE折起,使点D在面ABC上的射影K在直线AE上,当E从D运动到C,则K所形成轨迹的长度为( )
如图在矩形ABCD中,AB=2$\sqrt{3}$,BC=2,E为线段DC上一动点,现将△AED沿AE折起,使点D在面ABC上的射影K在直线AE上,当E从D运动到C,则K所形成轨迹的长度为( )
 如图在矩形ABCD中,AB=2$\sqrt{3}$,BC=2,E为线段DC上一动点,现将△AED沿AE折起,使点D在面ABC上的射影K在直线AE上,当E从D运动到C,则K所形成轨迹的长度为( )
如图在矩形ABCD中,AB=2$\sqrt{3}$,BC=2,E为线段DC上一动点,现将△AED沿AE折起,使点D在面ABC上的射影K在直线AE上,当E从D运动到C,则K所形成轨迹的长度为( )| A. | $\frac{2π}{3}$ | B. | $\frac{π}{3}$ | C. | $\frac{{\sqrt{6}+\sqrt{2}}}{3}$ | D. | $\frac{{\sqrt{6}+\sqrt{2}}}{2}$ |
19.若实数x,y∈R,则“x>0,y>0”是“xy>0”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
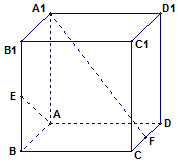 如图,正方体ABCD-A1B1C1D1的棱长为1,E、F分别是BB1和CD的中点.
如图,正方体ABCD-A1B1C1D1的棱长为1,E、F分别是BB1和CD的中点.