题目内容
在平面直角坐标系xOy中,圆C的参数方程为
(θ为参数),直线l经过点P(1,2),倾斜角α=
.
(Ⅰ)写出圆C的标准方程和直线l的参数方程;
(Ⅱ)设直线l与圆C相交于A、B两点,求|PA|•|PB|的值.
|
| π |
| 6 |
(Ⅰ)写出圆C的标准方程和直线l的参数方程;
(Ⅱ)设直线l与圆C相交于A、B两点,求|PA|•|PB|的值.
考点:参数方程化成普通方程
专题:坐标系和参数方程
分析:(Ⅰ)利用同角的三角函数的平方关系消去θ,得到圆的普通方程,再由直线过定点和倾斜角确定直线的参数方程;
(Ⅱ)把直线方程代入圆的方程,得到关于t的方程,利用根与系数的关系得到所求.
(Ⅱ)把直线方程代入圆的方程,得到关于t的方程,利用根与系数的关系得到所求.
解答:
解:(I)消去θ,得圆的标准方程为2+y2=16.…(2分)
直线l的参数方程为
,即
(t为参数) …(5分)
(Ⅱ)把直线的方程
代入x2+y2=16,
得(1+
t)2+(2+
t)2=16,即t2+(2+
)t-11=0,…(8分)
所以t1t2=-11,即|PA|•|PB|=11. …(10分)
直线l的参数方程为
|
|
(Ⅱ)把直线的方程
|
得(1+
| ||
| 2 |
| 1 |
| 2 |
| 3 |
所以t1t2=-11,即|PA|•|PB|=11. …(10分)
点评:本题考查了圆的参数方程化为普通方程、直线的参数方程以及直线与圆的位置关系问题,属于基础题.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案
相关题目
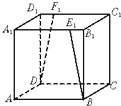 如图,正方体ABCD-A1B1C1D1中,E1、F1分别是A1B1、C1D1上的点,并且4B1E1=4D1F1=A1B1,则BE1与DF1所成角的余弦值是( )
如图,正方体ABCD-A1B1C1D1中,E1、F1分别是A1B1、C1D1上的点,并且4B1E1=4D1F1=A1B1,则BE1与DF1所成角的余弦值是( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知A、B、M三点不共线,对于平面ABM外任意一点O,若
+
=3
-
,则点P与A、B、M( )
| OB |
| OM |
| OP |
| OA |
| A、共面 | B、共线 |
| C、不共面 | D、不确定 |
如图是一个几何体的三视图,则该几何体的表面积是( )


A、98+3
| ||
B、98+6
| ||
C、88+3
| ||
D、88+8
|
 如图所示,在直三棱柱ABC-A1B1C1中,∠ACB=90°,AB=2,BC=1,
如图所示,在直三棱柱ABC-A1B1C1中,∠ACB=90°,AB=2,BC=1,