题目内容
 如图所示,在直三棱柱ABC-A1B1C1中,∠ACB=90°,AB=2,BC=1,AA1=
如图所示,在直三棱柱ABC-A1B1C1中,∠ACB=90°,AB=2,BC=1,AA1=| 3 |
(1)证明:A1C⊥平面AB1C1;
(2)若D是棱CC1的中点,在棱AB上是否存在一点E,使DE∥平面AB1C1;
(3)求三棱锥A1-AB1C1的体积.
考点:棱柱、棱锥、棱台的体积,直线与平面平行的判定,直线与平面垂直的判定
专题:空间位置关系与距离
分析:(1)根据几何体的性质得出AC1⊥A1C,A1C⊥B1C1,运用线面垂直的判定证明.
(2)E为AB中点,取AB1中点F,连接EF,ED,FC1,利用中位线,直线平面的平行定理证明.
(3)转换顶点V A1-AB1C1=V B1-AA1C1求解.
(2)E为AB中点,取AB1中点F,连接EF,ED,FC1,利用中位线,直线平面的平行定理证明.
(3)转换顶点V A1-AB1C1=V B1-AA1C1求解.
解答:
证明:(1)∵在直三棱柱ABC-A1B1C1中,∠ACB=90°,AB=2,BC=1,AA1=
.
∴AC=
,C1C⊥B1C1,
∵AA1=
∴四边形ACC1A1为正方形,
∴AC1⊥A1C,
∵AC,BC,CC1两两垂直,BC∥B1C1
∴B1C1⊥面ACC1A1,
∵A1C?面ACC1A1,
∴A1C⊥B1C1,
∵B1C1∩AC1=C1,AC1⊥A1C,A1C⊥B1C1,
∴A1C⊥平面AB1C1;
解:(2)在棱AB上存在一点E,使DE∥平面AB1C1;
E为AB中点,
∵取AB1中点F,连接EF,ED,FC1,
∴EF∥BB1,DC1∥BB1,EF=
BB1,C1D=
BB1,
∴EF∥DC1,EF=DC1
∴四边形EFCD1,
∴ED∥FC1,
∵FC1?平面AB1C1,DE?平面AB1C1
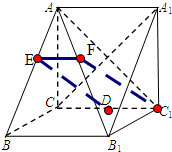
∴DE∥平面AB1C1;
解:(3)∵B1C1⊥面ACC1A1,四边形ACC1A1为正方形,AA1=
∴V A1-AB1C1=V B1-AA1C1=
×
×A1C1×AA1×B1C1=
×
×
×
×1=
| 3 |

∴AC=
| 3 |
∵AA1=
| 3 |
∴四边形ACC1A1为正方形,
∴AC1⊥A1C,
∵AC,BC,CC1两两垂直,BC∥B1C1
∴B1C1⊥面ACC1A1,
∵A1C?面ACC1A1,
∴A1C⊥B1C1,
∵B1C1∩AC1=C1,AC1⊥A1C,A1C⊥B1C1,
∴A1C⊥平面AB1C1;
解:(2)在棱AB上存在一点E,使DE∥平面AB1C1;
E为AB中点,
∵取AB1中点F,连接EF,ED,FC1,
∴EF∥BB1,DC1∥BB1,EF=
| 1 |
| 2 |
| 1 |
| 2 |
∴EF∥DC1,EF=DC1
∴四边形EFCD1,
∴ED∥FC1,
∵FC1?平面AB1C1,DE?平面AB1C1

∴DE∥平面AB1C1;
解:(3)∵B1C1⊥面ACC1A1,四边形ACC1A1为正方形,AA1=
| 3 |
∴V A1-AB1C1=V B1-AA1C1=
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 3 |
| 3 |
| 1 |
| 2 |
点评:本题考查了空间几何体的性质定义,直线平面的平行垂直问题,距离,体积的求解,属于中档题,难度不大.

练习册系列答案
 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目
 如图,在四面体ABCD中,AB=1,AD=2
如图,在四面体ABCD中,AB=1,AD=2| 3 |
| π |
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知函数f(x)=x-1-lnx,若不等式f(x)≥bx-2对任意x∈(0,+∞)恒成立,则实数b的取值范围是( )
A、(-∞,1-
| ||
B、[1-
| ||
C、(0,1-
| ||
D、[1-
|